第179問の解答
1.問題 [整数の性質]
| ある長距離徒歩大会に出場したマサル君、トモエさん、ツヨシ君は、 それぞれ毎時3km、毎時4km、毎時5kmで歩くことにしました。 この大会では、コース脇に「あと○km」という標識がスタートから1kmごとに表示されています。 それを見ながら歩いていたマサル君は、 「あ、スタートからの経過時間(単位:時間)と残りの距離が同じだ....。」 とあるときに思ったそうです。 また、トモエさん、ツヨシ君もそれぞれ同じこと道中に思ったそうです。 さて、この大会は、全長何kmの距離を歩くことになっていたのでしょうか。 考えられる距離の中で最短のものを答えてください。 |
2.解答例1(多数)
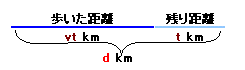
題意のような状況になるとき、歩く速度をvkm/時、歩いた時間をt時間、コース長をdkmとすると、
vt+t=d、すなわち(v+1)t=dが成り立ちます。従って、3人とも同様な状況が発生したので、それぞれ歩いた時間をt1,t2,t3とすると、
4×t1=5×t2=6×t3=d。題意より、t1,t2,t3とも整数なので、dは4,5,6の倍数でなければならない。
従って、最短距離は最小公倍数である60kmである。
答:60Km
以上