第１８１問の解答

---

１．問題　［平面図形］

左図は、ＡＤ＝２８cm、ＡＢ＝２１cmの長方形ＡＢＣＤの辺上にＰ、Ｑ、Ｒ、Ｓをとったところを示しています。 　いま、ＰＳとＱＲと対角線ＢＤはそれぞれ平行、またＰＱとＳＲも平行です。 また、四角形ＰＱＲＳの面積は２４０cm2であるといいます。 　このとき、ＡＰの長さを求めてください。ただし、ＡＰはＰＢよりも長いものとします。

---

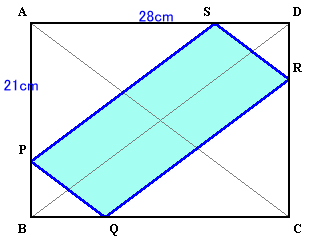２．解答例１（Hamayanさん他多数）

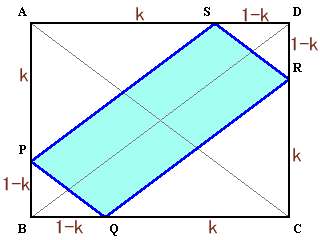
AP/AB=k、長方形ＡＢＣＤの面積＝Ｓとします。

△ＡＰＳと△ＡＢＤは相似で相似比はｋ：１。
よって、△ＡＰＳ＝△ＡＢＤ×ｋ²＝1/2×Ｓ×ｋ²
同様に、△ＣＱＲ＝△ＣＢＤ×ｋ²＝1/2×Ｓ×ｋ²

また、△ＢＰＱと△ＢＡＣは相似で相似比はｋ-1：１。
よって、△ＢＰＱ＝△ＢＡＣ×（ｋ-1）²＝1/2×Ｓ×（ｋ-1)²
同様に、△ＤＳＲ＝△ＤＡＣ×（ｋ-1)²＝1/2×Ｓ×（ｋ-1)²

以上から、
△ＡＰＳ＋△ＣＱＲ＋△ＢＰＱ＋△ＤＳＲ＝Ｓ×（ｋ²＋（ｋ-1)²)、
ｋ²＋（ｋ-1)²＝（Ｓ−２４０）／Ｓ、
２ｋ²−２ｋ＋１＝１−２４０／（２８×２１）、
ｋ²−ｋ＋（２/７）×（５/７）＝０、
（ｋ−２/７）（ｋ−５/７）＝０、
よって、ｋ＝２/７、５/７。

題意より、ＡＰ＞ＰＢだからｋ＞ｋ−１。よって、ｋ＞１/２。
従って、ｋ＝５/７が題意に適します。

よって、ＡＰ＝ＡＢ×５/７＝２１×５/７＝１５ｃｍとなります。

答：１５ｃｍ

　以上

---

３．解答例２（むらかみさん他）

四隅の△ＡＰＳ、ＢＰＱ、ＣＱＲ、ＤＳＲを長方形ＡＢＣＤの中に折り込み、
それぞれ△ＥＰＳ、ＨＰＱ、ＧＱＲ、ＦＳＲとします。

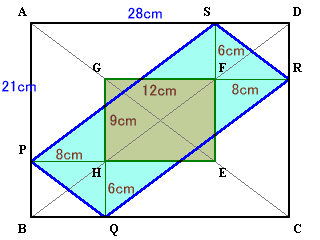
Ｅ、Ｇは対角線ＡＣ上、Ｈ、Ｆは対角線ＢＤ上にあり、四角形ＧＨＥＦは長方形になります。

△ＡＰＳ、ＢＰＱ、ＣＱＲ、ＤＳＲの面積の和は、平行四辺形ＰＱＲＳに重複している四角形ＧＨＥＦの面積を加えたものになります。

△ＡＰＳ＋△ＢＰＱ＋△ＣＱＲ＋△ＤＳＲ＝平行四辺形ＰＱＲＳ＋長方形ＧＨＥＦ

長方形ＡＢＣＤ−平行四辺形ＰＱＲＳ＝平行四辺形ＰＱＲＳ＋長方形ＧＨＥＦ、
２８×２１−２４０＝２４０＋長方形ＧＨＥＦ、
よって、長方形ＧＨＥＦ＝５８８−４８０＝１０８ｃｍ²。

ここで、対角線の交点をＯとすると、
△ＯＡＢとＯＧＨは相似、ＧＨ：ＡＢ＝ＯＧ：ＯＡ、
△ＯＡＤとＯＧＦは相似、ＧＦ：ＡＤ＝ＯＧ：ＯＡ。

よって、ＧＨ：ＧＦ＝ＡＢ：ＡＤ＝２１：２８＝３：４。

１０８＝（３×３）×（３×４）より、ＧＨ＝９ｃｍ、ＧＦ＝１２ｃｍ。

ＳＦ＝ＨＱより、ＳＦ＝（ＡＢ−ＧＨ）／２＝（２１−９）／２＝６ｃｍ、
従って、ＡＰ＝ＳＦ＋ＧＨ＝６＋９＝１５ｃｍ。

---