第１８２問の解答

---

１．問題　［規則性］

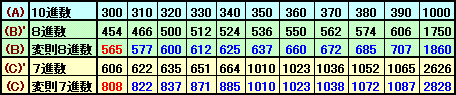
１から１０００までの数字があります。これを上図のように３通りの方法で番号を付けました。 （Ａ）１番から１０００番まで順番に番号を付ける。 （Ｂ）１番から順番に番号を付ける。ただし、４と９は使わずに番号をふる。 （Ｃ）１番から順番に番号を付ける。ただし、４と６と９は使わずに番号をふる。 （１）（Ａ）で２１６番だった数字は、（Ｃ）では何番になったでしょうか。 （２）ある数字の番号は、（Ａ）→（Ｂ）のときに百の位の数が２増え、一の位の数が５増えました。 　　（Ｂ）→（Ｃ）のときにはさらに、百の位、一の位ともに３増えたそうです。 　　では、この数字は（Ｃ）では何番になったでしょうか。

---

２．解答例１
（わかさひ君、ヒデー王子さん、ＴＯＲＡさん、えくさーつー(爆)(阿)さん、YokoyaMacさん、中学への算数学コンさん他多数）

題意より、（Ａ）、（Ｂ）、（Ｃ）は、それぞれ数字が１０個、８個、７個で数えるので、１０進数、８進数、７進数で計算すればよいことになる。

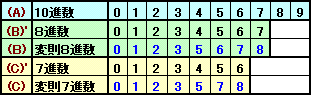
ただし、数字は通常の数字でなく、上図のように、（Ｂ）では４，９、（Ｃ）では４，６，９を使用しない変則な数え方をします。

（設問１）

２１６（10進数）を７進数に直すのは、下図のように次々と７で割り、余りを求めていけばいい。

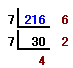
２１６(10進数)＝４２６（７進数）＝５２８（変則７進数）

答：５２８

（設問２）

一位の数字は、１０進数→変則８進数→変則７進数に応じて、＋５，＋３するということは、１０進数→変則７進数で＋８となることから、０→５→８のケースしかありえない。・・・(*１)

百位の数字は、１０進数→変則８進数→変則７進数に応じて、＋２，＋３することから、０→２→５、３→５→８の２ケースが考えられる。・・・(*２)

求める数は、１０進数で１から１０００までだから、可能性のあるのは、次の数。
　３００，３１０，３２０，３３０，３４０，３５０，３６０，３７０，３８０，３９０，１０００

これらの数について、変則８進数、変則７進数を計算すると、次の通り。

このうち、題意を満たすのは３００(10進数)＝５６５（変則８進数）＝８０８（変則７進数）のみである。

答：８０８

（別解）

(*１)より、１０進数→８進数→７進数では、０→４→６となり、
求める数ｘは、１０で割った余りが０、８で割った余りが４、７で割った余りが６となる。

よって、ｘ＝１０ｎ＝８ｍ＋４＝７ｌ＋６　と書ける。

１０ｎ＝８ｍ＋４より、５ｎ＝４ｍ＋２、ｎ＝４（ｍ−ｎ）＋２、
従って、ｓ＝ｍ−ｎとおくと、ｎ＝４ｓ＋２、ｍ＝５ｓ＋２、ｘ＝４０ｓ＋２０を得る。

４０ｓ＋２０＝７ｌ＋６より、３５ｓ＋５ｓ＝７ｌ−１４、５ｓ＝７（ｌ−ｓ＋２）、
ｓ＝ｌ−ｓ＋２とおくと、５ｓ＝７ｔ、従って、ｓは７の倍数となり、ｓ＝７ｐ、
よって、ｌ＝１４ｐ−２、と書ける。

従って、ｘ＝２８０ｓ＋２０と書ける。
このうち、１≦ｘ≦１０００を満たすのは、ｘ＝２０、３００、５８０、８６０。
さらに(*２)を満たすのは、３００のみとなる。

　以上

---