第１８４問の解答

１．問題　［平面図形］

問題図
正三角形ＡＢＣがあります。辺ＡＣの中点Ｍと頂点Ｂを結び、線分ＢＭ上に点Ｄを取ります。
さらに、点ＥをＭの反対側にとって正三角形ＡＤＥを作ります。

また、辺ＥＤと辺ＡＢの交点をＦとします。
　このとき、ＥＦ：ＦＤ＝３：１となりました。

　正三角形ＡＢＣの面積が６cm2であるとき、四角形ＡＥＢＤの面積を求めてください。

　

２．解答例１（ヒデー王子さん、うっしーさん、長野美光さん他多数）

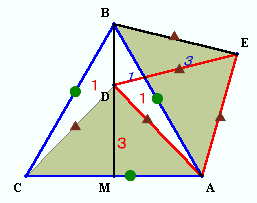
図１
参考図1		 図２
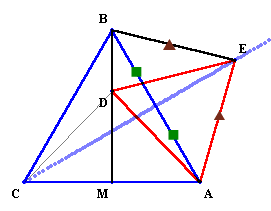
参考図2

△ＡＢＥと△ＡＣＤについて、ＡＢ＝ＡＣ、ＡＥ＝ＡＤ、および∠ＢＡＥ＝６０−∠ＤＡＢ＝∠ＣＡＤより△ＡＢＥ≡△ＡＣＤ。

よって、求める四角形ＡＥＢＤの面積は、四角形ABDCと同じになる。

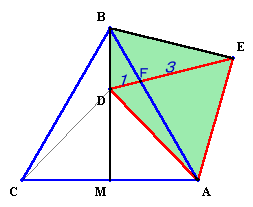
ＤＦ：ＦＥ＝１：３だから、△ABD：△AＣＤ＝△ABD：△AＢＥ＝１：３。

△ABD=△BDCなので、四角形ABDCの面積＝△ABC×4/5＝６×4/5＝４．８ｃｍ2になります。 

答：４．８ｃｍ2

　以上

（参考）図２のとおり、点ＤがＢＭ上のどんな位置にあっても、ＥＡ＝ＥＢとなるので、Ｅの軌跡は、ＡＢの垂直二等分線上にあることが分かる。