第186問の解答
1.問題 [整数の性質]
| エンピツとノートが同じ数だけあります。 エンピツはA組の13人で、ノートはB組の14人で分けました。(1人あたりの数ができるだけ多くなるように、かつみんな同じ数ずつ渡るようにします。)すると、A組の生徒が持っているエンピツの数と、B組の生徒が持っているノートの数が等しくなったそうです。 では、エンピツの総数(=ノートの数)として考えられる数は何通りあるでしょうか。 ※・・・もちろん、エンピツやノートが余っちゃうこともあります。 ※・・・どの生徒も必ず1本(1冊)はもらうものとします。 |
2.解答例1(YokoyaMacさん、TORAさん、Miki Sugimotoさん、長野美光さん、清川育男さん他)
エンピツの総数(=ノートの数)をn、
A組の生徒が持っているエンピツの数=B組の生徒が持っているノートの数をa
とすると、
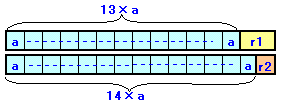
n=13a+r1=14a+r2 (0<a、0≦r1≦12、0≦r2≦13)
と書ける。
上記式よりnから、a、r1、r2は一意的に決まり、またa、r1を決めればn、r2は一意的に決まる。
0≦r2=r1−a≦13 より、a≦r1≦12。
よって、
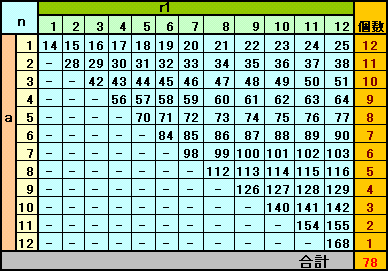
a=1のとき、r1=1、2、・・・、12の12通り、
a=2のとき、r1=2、・・・、12の11通り、
・・・・
a=12のとき、r1=1の1通り、
合計12+11+・・・+1=(1+12)/2×12=78通りとなる。
答:78通り
以上