第１８７問の解答

１．問題　［空間図形］

問題図

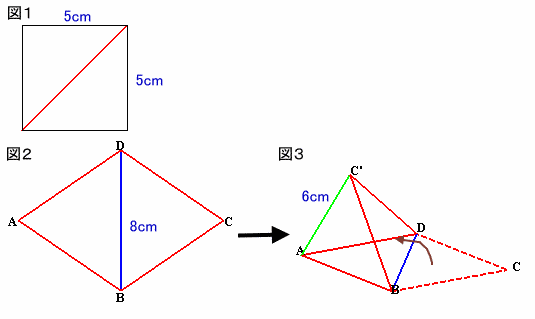
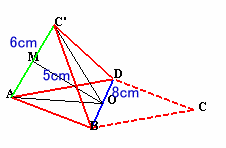
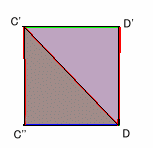
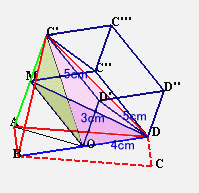
　上の図２のような、ＡＢ、ＢＣ、ＣＤ、ＤＡの長さがすべて、１辺５cmの正方形の対角線（図１）の長さと等しく、ＤＢ＝８cmである四角形の紙があります。

　この紙を、図３のようにＤＢを折り目にして折り曲げ、ＡＣ'（Ｃ'はＣの移動先の点）＝６cmになるようにしました。

　このとき、三角錐Ｃ'ＡＢＤの体積を求めてください。

２．解答例１（ぶぶおパパ さん、東日本に貢献？さん、ヒデー王子さん、武田浩紀さん他）

ＡＣの中点をＭ、ＢＤの中点をＯとすると、三角錐Ｃ'ＡＢＤは、面Ｃ'ＡＯに関して対称、ＢＤは面Ｃ'ＡＯと直交、よってＭＯとＢＤも直交していることが分かる。
また、ＡＣ'とＭＯも直交している。

参考図01

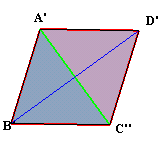
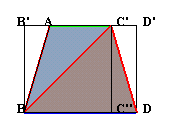
さて、ＢＤを含みＡＣ'に平行な平面１と、ＡＣ'を含みＢＤに平行な平面２を考える。
Ａ、Ｃ'から平面１に下ろした垂線の足をＡ'、Ｃ''とし、Ｂ、Ｄから平面２に下ろした垂線の足をＢ'、Ｄ'とする。

平面図
参考図1		 側面図
参考図2
（参考）マウスでドラッグして下さい。
正面図
参考図3		 俯瞰図
参考図4

上図のように各点を結ぶと、上の面ＡＢ'Ｃ'Ｄ'および底面Ａ'ＢＣ''Ｄは、対角線の長さが６ｃｍと８ｃｍの菱形になり、対角線は直交している。

従って、この菱形を４等分した三角形は、辺の長さが３ｃｍ、４ｃｍ、５ｃｍの直角三角形となることから、菱形の１辺の長さは５ｃｍと分かる。

よって、側面は全て大きさが同じ長方形になる。
この長方形の横の長さ（例えばＢＣ''）は菱形の１辺５ｃｍ、対角線の長さは図１の正方形の対角線の長さと等しいことから、この側面は結局正方形となり、高さ（例えばＣ'Ｃ''）も５ｃｍとなる。

以上から、三角錐Ｃ'ＡＢＤの体積は、
上記菱形を底面とする四角柱の体積（1/2×６×８×５＝１２０cm3）から
同じ大きさの４つの三角錐の体積（1/4×６×８×５×1/3＝２０cm3）を除いたものとなり、
１２０−２０×４＝４０cm3と分かる。

答：４０cm3

　以上

３．解答例２（ありさのお父さん、大西俊郎さん、H.Takaiさん他）

ＭＯ、ＭＤを底面に含み、高さがＭＣ'となるような直方体を考える。

参考図01 参考図02

ＯＤ'＝３ｃｍ、ＯＤ＝４ｃｍなので、対角線ＤＤ'＝５ｃｍとなる。
ところが、C'ＤＤ'は直角三角形で１辺が５ｃｍ、斜辺が図１の対角線と同じ長さなので、もう一方の辺Ｃ'Ｄ'＝５ｃｍと分かる。

上図より、三角錐Ｃ'ＭＯＤの体積は求める三角錐の1/4、
　Ｃ'ＭＯＤの体積＝1/2×５×４×３×1/3＝１０ｃｍ3　だから
　Ｃ'ＡＢＤの体積＝１０×４＝１０ｃｍ3となる。

４．解答例３（Hamayanさん、わかさひ君、長野美光さん他）

参考図01

ＡＯ2＝ＡＤ2−ＯＤ2＝２×５2−４2＝３４、
ＭＯ2＝ＡＯ2−ＡＭ2＝３４−３2＝２５、よってＭＯ＝５ｃｍと分かる。

Ｃ'ＡＢＤは、２つの三角錐Ｃ'ＡＯＤとＣ'ＢＯＤに２等分されるので、
Ｃ'ＡＢＤの体積＝（1/2×６×５×４×1/3）×２＝４０ｃｍ3と分かる。