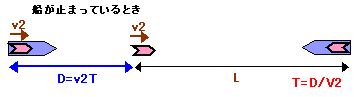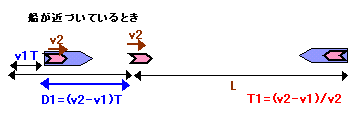第188問の解答
1.問題 [速さの問題・ドップラー効果]
| 2隻の舟、マサル号とトモエ号があります。 マサル号はA島からB島に向かって、トモエ号はB島からA島に向かって同じ速度で進行しています。(最初、両者は近づきつつあります) 2隻の舟からは、一定時間ごとにハトを相手の舟に向かって飛ばしています。 このとき、同じ時間にマサル号とトモエ号を飛び立った2羽のハトが出会う周期を測ったところ、最初7分ごとでしたが、途中からは11分ごとになったそうです。 |
2.解答例1
2隻の船およびハトどうしの相対速度が問題になるので、トモエ号およびトモエ号のハトは止まっているものとして考えて良い。このとき、相対速度は、それぞれ2倍になるが、速度比は変わらない。
さて、マサル号が止まっているときをまず考えてみよう。
船の速度をv1m/s、ハトの速度をv2m/s、マサル号からT分周期でハトが飛び立つものとする。ハトが飛び立ってからT分経過し、次のハトが飛び立とうとするとき、前のハトはv2・Tm進んでいる。次のハトがその地点にいくまでには、v2・T/v2=T分かかる。
その後の経過は、前のハトと全く同じだから、結局トモエ号にいるハトと出会う周期は、マサル号を飛び立つ周期と同じT分である。
次に、マサル号がトモエ号に近づいているときを考える。
ハトが飛び立ってからT分経過し、次のハトが飛び立とうとするとき、前のハトはv2・Tm進んでいる。ところが、マサル号もv1・Tm進んでいるので、次のハトがその地点にいくまでには、(v2-v1)・T/v2分となる。
その後の経過は、前のハトと全く同じだから、結局トモエ号にいるハトと出会う周期は、
(v2-v1)・T/v2分である。
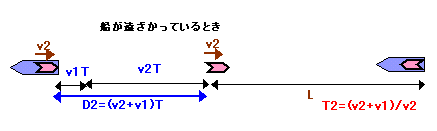
同様に、マサル号がトモエ号から遠ざかるときを考える。
ハトが飛び立ってからT分経過し、次のハトが飛び立とうとするとき、前のハトはv2・Tm進んでいる。ところが、マサル号もv1・Tm遠ざかっているので、次のハトがその地点にいくまでには、(v2+v1)・T/v2分となる。
その後の経過は、前のハトと全く同じだから、結局トモエ号にいるハトと出会う周期は、
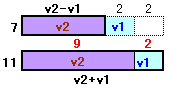
(v2+v1)・T/v2分である。以上から、(v2-v1)・T/v2=7、(v2+v1)・T/v2=11となる。
従って、(v2-v1):(v2+v1)=7:11となる。
上図から、v2=(11+7)/2=9分、v1=(11−7)/2=2分。
よって、v2:v1=9:2、すなわち、ハトの速さは船の4.5倍となります。