第１８９問の解答

１．問題　［空間図形］

正面から見た図
問題図3		 上から見た図
問題図1		 右から見た図
問題図2
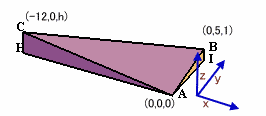
　上図は、ある巨大な立体の、「上から」「正面から」「右から」見た図（注・正面および右からの図は、それぞれ一番手前の面を描いています）をそれぞれ並べたものです。この立体は、面ＡＢＣ、面ＡＣＨ、面ＡＢＩが平面で出来ています。

　Ａ地点からいろいろな方向に向かってまっすぐ進むとき、Ｂに向かうと勾配は１／５です。
また、最も坂が急になる方向だと、勾配は１／４になります。

　さて、図中のＣＨの長さは何ｍでしょうか。

２．解答例１（Taroさん、ありさのお父さん、たなかさん、Hamayanさん）

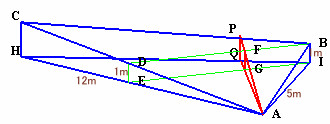
題意より、問題の立体は下図のようなものと分かる。

参考図1

Ｂを通り高さが１ｍの点よりなる直線を考え、ＡＣとの交点をＤ、ＤからＡＨに下ろした足をＥとする。

また、ＩＥ上の点ＧをＡＧ＝４ｍとなるように取り、ＡＧの延長とＨＩの交点をＱとし、Ｇ、Ｑを垂直に伸ばした点と平面ＡＢＣとの交点をＦ、Ｐとする。

俯瞰図
参考図2		 上から見た図
参考図3

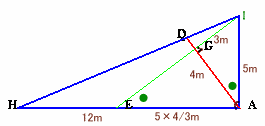
ＡＰが最大勾配となるとき、ＡＱとＩＥは直交するので、三角形ＡＩＧは３辺が３、４、５ｍの直角三角形となる。

三角形ＥＩＡは三角形ＡＩＧと相似なので、ＡＥ＝ＡＩ×ＡＧ／ＩＧ＝５×４／３＝２０／３ｍとなる。

三角形ＡＣＨとＡＤＥは相似なので、
　ＣＨ＝ＤＥ×ＡＨ／ＡＥ＝１×１２／（２０／３）＝１．８ｍとなります。

答：１．８ｍ

　以上

３．解答例２（長野美光さん他）

ＣＢを延長し平面ＡＩＨと交わる点をＤ、ＨＡの延長線上にＦをＤＦとＡＢが平行となるように引く。また、ＩからＤＦに下ろした垂線の足をＥとする。

俯瞰図
参考図4		 上から見た図
参考図5
（参考）マウスでドラッグして下さい。

ＡＤ上の点ＫでＢＫが最大勾配となるのは、ＩＫとＡＤが直交するときなので、題意よりＢＫ＝４ｍ、ＡＫ＝３ｍと分かる。

ＢＥ＝１２とすると、
ＤＥ＝ＢＥ×ＡＢ／ＡＨ＝１２×５／１２＝５、ＤＦ＝ＢＥ×ＡＫ／ＢＫ＝１２×３／４＝９。

よって、ＣＨ＝ＢＩ×ＨＤ／ＢＤ＝ＢＩ×ＤＦ／ＤＥ＝１×９／５＝１．８ｍ。

４．解答例３（M.Hossieさん、YokoyaMacさん他）

下図のように、Ａを原点とする座標系で考える。

参考図6

平面ＡＢＣはＡ（0,0,0）、Ｂ（0,5,1）、Ｃ（-12,0,h）を通るので、(-5/12)hx + y - 5z = 0 で表せる。
ｋ＝5/12hとおくと、-ｋx + y - 5z = 0 ・・・（１）となる。

底面ＡＨＩ上の点でＰ（ｃｏｓθ、ｓｉｎθ、０）を垂直に伸ばし、平面ＡＢＣと交わる点をＱ（ｃｏｓθ、ｓｉｎθ、ｚ）とする。

（１）より、ｚ＝（−ｋｃｏｓθ＋ｓｉｎθ）／５＝√（１＋ｋ2）／５×ｃｏｓ（θ＋α）と書ける。

この最大値が最大勾配の１/４になるので、√（１＋ｋ2）／５＝１/４、
ｋ2＝９/１６、よってｋ＝３/４。

従って、ｈ＝１２/５×３/４＝１．８ｍとなる。

５．解答例４（きょえぴさん他）

解答例３同様、Ａを原点とする座標系で考える。

HI,CB上にそれぞれ点P(-12t,5(1-t),0),Q(-12t,5(1-t),ht+1-t)をとる。（h>0）

点Aから点Qに向かうときの勾配はPQ/APである。
これをｔの関数としてf(t)とすると、　f(t) = (ht+1-t)/(169t2+25-50t)1/2　と表せる。

微分して、
　f'(t)= -(-25h+25ht+144t)/(169t2+25-50t)3/2=0より、
　t = 25h/(25h+144)　のとき最大

最大値　f(25h/(25h+144))=(25h2+144)/60=1/4を解くと、h=9/5,-9/5を得る。
よって、h=9/5=１．８ｍとなる。

（参考）y=f(t)のグラフ

h=1.8のとき、最大値＝0.25になっている。

参考図9