第１９０問の解答

１．問題　［差集め算］

　ツヨシ君、トモエさん、マサル君の３人がある距離のかけっこをすることにしました。

　３人の走る速さを分速で比べると、トモエさんはマサル君よりも分速２０ｍ速く、ツヨシ君はトモエさんよりも分速３０ｍ速いそうです。

　３人が同時にスタート地点を出発したところ、第１位のツヨシ君がゴールしてから５分後にトモエさんがゴールし、トモエさんがゴールした５分後にマサル君がゴールしたそうです。

　では、３人がかけっこした距離は何ｍでしょうか？

２．解答例１（きょえぴさん、M.Hossieさん他）

参考図1

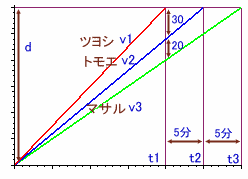
ツヨシ君がゴールしたとき（t1分後）、トモエさん、マサル君の残りの道のりの比は、
３０：（２０＋３０）＝３０：５０になります。 

それぞれをトモエさんは５分（t2-t1）、マサル君は10分（t3-t1）で走ったのですから、
彼らの速さの比は３０/５：５０/１０＝６：５になります。 

この比の差1が２０m/分に相当するのでトモエさんは１２０m/分（v2）、マサル君は１００m/分（v3）、従ってツヨシ君は１５０m/分（v1）の速さです。 

さらにトモエさんとマサル君のゴールまでの所要時間は、速さの逆比なので 
１/６：１/５＝５：６です。 

この比の差1が5分に相当しますから、トモエさんは25分（t2）、マサル君は30分（t3）、従ってツヨシ君は、25分（t1）かかります。 

したがって、求める道のりは、
　ツヨシ君：１５０×２０＝３０００ｍ
　トモエさん：１２０×２５＝３０００ｍ
　マサル君：１００×３０＝３０００ｍ
になります。 

答：３０００ｍ

　以上

３．解答例２（14ozLIDさん、中村明海さん、Miki Sugimotoさん、うっしーさん他）

t1=t,t2=t+5,t3=t+10,v3=v,v2=v+20,v1=v+50とおきます。

　t(v+50)=d　　　　・・・（１）
　(t+5)(v+20)=d　　・・・（２）
　(t+10)v=d　　　　・・・（３）
より、
　vt+50t=d　　　　　　・・・（４）
　vt+20t+5v+100=d　・・・（５）
　vt+10v=d　　　　　　・・・（６）

（４）-（６）より、50t-10v=0、よってv=5t。　・・・（７）
（４）-（５）より、30t-5v-100=0、（７）より、30t-5(5t)=100、よってt=20を得る。

従って、v=5×20＝100、d=20×（100+50）＝３０００mとなります。

　

または、t1=d/(v+50)、t2=d/(v+20)、t3=d/vおよび(t1+t3)/2=t2より、
　1/(v+50)+1/v=2/(v+20)

よって、{v+(v+50)}/{(v+50)v}=2/(v+20)、(2v+50)(v+20)=2v(v+50)、
　v2+45v+500=v2+50v、5v=500、よってv=100を得る。　

d(1/100-1/120)=5、d×(120-100)=5×100×120、よってd=３０００mを得る。