第１９１問の解答

---

１．問題　［空間図形］

マサルさん、トモエさんの２人が直線距離で１８００ｍ離れたＡ地点、Ｂ地点にいます。 　あるとき、上空を飛んでいた飛行機（左図Ｐ１）をマサルさん、トモエさんが同時に見たところ、マサルさんは西の方角に仰角（見上げる角度）４５゜で、トモエさんは北の方角に傾き４/３の仰角で見えたそうです。 　その後、マサルさんが飛行機を目で追いかけたところ、９秒後にはちょうどトモエさんがいるＢ地点の方角に、さらにその１６秒後には南の方角に飛行機は見えたそうです。 （１）　飛行機は高度何ｍのところを飛んでいたでしょうか。 （２）　この飛行機は秒速何ｍで飛んでいるでしょうか。

---

２．解答例１（たなかさん、わかさひ君、ありさのお父さん他）

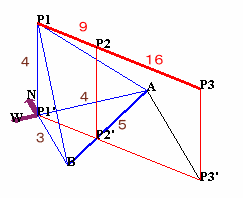
９秒後の飛行機の位置をP1、その１６秒後の位置をP2とし、これらの真下の位置をP1'、P2'とします。

（参考）マウスでドラッグして下さい。

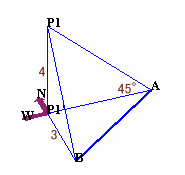
ＢＰ１の長さを３とすると、Ｐ１・Ｐ１'＝ＡＰ１'＝４、
よって三角形Ｐ1'・Ａ・Ｂは辺の長さが３：４：５の直角三角形となり、
ＡＢ＝５となります。

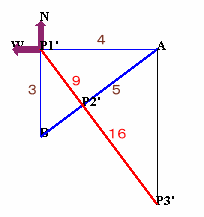
三角形Ｐ２'・Ｐ１'・Ｂと三角形Ｐ２'・Ｐ３'・Ａは相似なので、
　Ｐ１'・Ｂ：Ｐ３'・Ａ＝Ｐ１'・Ｐ２：Ｐ２'・Ｐ３'＝９：１６、
よって、Ｐ３'・Ａ＝３×１６/９＝１６/３。

従って、Ｐ１'・Ａ：Ｐ３'・Ａ＝４：１６/３＝３：４。
よって、三角形Ｐ1'・Ｐ３'・Ａは辺の長さが３：４：５の直角三角形となり、
　Ｐ１'・Ｐ３'＝４×５/３＝２０/３。

さて、ＡＢ＝１８００ｍだから、Ｐ１・Ｐ１'＝１８００×４/５＝１４４０ｍ、
　Ｐ１'・Ｐ３'＝１８００×（２０/３）/５＝２４００。

この間を飛行機は６＋９＝２５秒で飛んだのだから、
　飛行機の速度＝２４００/２５＝９６ｍ/秒と分かります。