第192問の解答
1.問題 [平面図形]
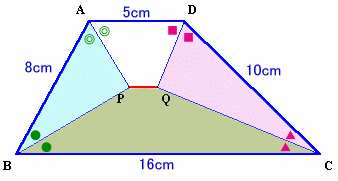 |
|
2.解答例1
(CRYING DOLPHINさん、Hamayanさん、わかさひ君、長野 美光さん、うっしーさん、BOSさん他)
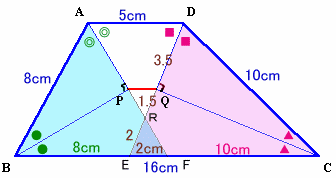
APの延長と辺BCの交点をF、DQの延長と辺BCの交点をEとします。
ADとBCが平行だから、角DAF=角AFB。
よって、三角形ABPと三角形FBPは2角が等しいので相似となり、辺BPが共通なことから合同となります。
従って、角APB=角FPB=90°、すなわち三角形ABPと三角形FBPは合同な直角三角形となります。
これから、BF=AB=8cmと分かります。同様に、三角形DCQと三角形ECQは合同な直角三角形、EC=DC=10cmとなります。
従って、EF=BF+EC−BC=8+10−16=2cm。
三角形ARDとFREは相似だから、DR:RE=AD:FE=5:2。
よって、DQ=QEより、DQ:QR=3.5:1.5=7:3。さて、AP=PF、DQ=QEより、Pから辺BCへ下ろした垂線の長さ(h2とします)、QからBCへ下ろした垂線の長さはどちらも台形ABCDの高さ(h1とします)の半分で等しい。
よって、PQはADおよびBCと平行と分かります。よって、三角形ARDとPRQは相似となり、PQ:AD=RQ:RD=3:10。
従って、PQ=AD×3/10=5×3/10=1.5cm。台形ABCDの面積をS1、台形PBCQの面積をS2とすると、
S1=1/2×(AD+BC)×h1=1/2×(5+16)×h1=21/2×h1。
S2=1/2×(PQ+BC)×h2=1/2×(1.5+16)×h1=17.5/2×h2
=35/4×h2。よって、S1/S2=21/2×h1/35/4×h2=6/5×h1/h2=12/5=2.4倍
と分かります。