第１９３問の解答

１．問題　［平面図形］

図１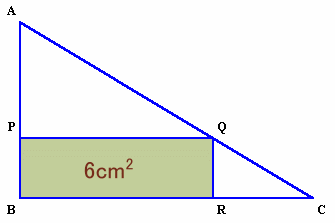
問題図		 図２
問題図2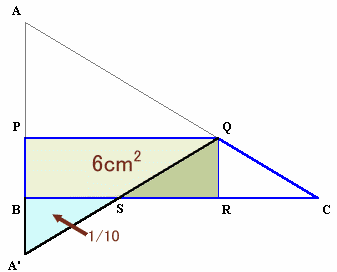
図１のような直角三角形ＡＢＣがあります。ＡＣ上に点Ｑをとり、長方形ＰＢＲＱを作ると面積は６ｃｍでした。
ＰＱを軸にして、三角形ＡＰＱを折り返して出来る三角形Ａ'ＰＱが、元の三角形ＡＢＣよりはみ出した部分をＡ'ＢＳとすると、この面積は、ＡＢＣの面積の1/10でした。

では、三角形ＡＢＣの面積は、何ｃｍ2でしょうか？

２．解答例１

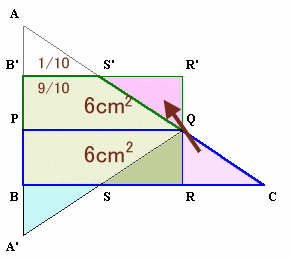
ＰＱを軸として、長方形ＰＢＲＱを折り返してできる長方形をＰＢ'Ｒ'Ｑとします。

参考図

三角形ＱＲＣとＱＲ'Ｓ'は合同、三角形ＡＢＳとＡＢ'Ｓ'は合同。

よって、長方形Ｂ'ＢＲＲ'の面積＝三角形ＡＢＣの面積×９/１０、
　　　三角形ＡＢＣの面積×１０/９
　＝長方形Ｂ'ＢＲＲ'の面積×１０/９
　＝１２×１０/９
　＝４０/３

答：４０/３ｃｍ2

　以上