第194問の解答
1.問題 [平面図形]
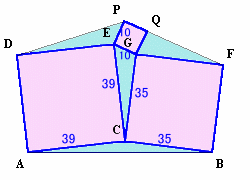 |
3つの正方形があり、それぞれの一辺の長さは39cm、35cm、10cmです。
これら3つの正方形と、三角形4つとを組み合わせて左の図のような図形を作りました。
このとき、三角形4つ分の面積を求めてください。 |
|
2.解答例1(たなかさん、sambaGREENさん、KINさん、長野美光さん、永弘さん、きょえぴさん、中村明海さん、他多数)
4つの三角形の面積が等しいことが次のようにして分かります。
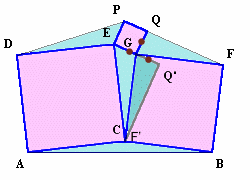
三角形GQFを90度回転してGF'をGCに合わせると、
角EGC+角QGF=180度より、EGQ'は1直線上に並びます。
EG=GQ'で、高さは共通だから、三角形EGCの面積=三角形GQ'F'の面積。
(三角形の面積=2辺の長さの積×sin(挟む角)÷2 からも分かります)
真ん中の三角形EGCは、三辺の長さが39、35、10なので、ヘロンの公式により、a=39,b=35,c=10,s=(39+35+10)/2=42として、
三角形EGCの面積=√{s(s-a)(s-b)(s-c)}=√{42・3・7・32}=168
よって、求める面積=168×4=672
(ヘロンの公式) (Hamayanさんによる)
(a+b+c)/2=sとおくと、
S
=(1/2)absinC
=(1/2)ab√(1-cos2C)
=(1/2)ab√[1-{(a2+b2-c2)/2ab}2]
=(1/2)ab√[{(2ab)2-(a2+b2-c2)2}/(2ab)2]
=(1/4)√[(2ab+a2+b2-c2)(2ab-a2-b2+c2)]
=(1/4)√[{(a+b)2-c2}{c2-(a-b)2}]
=(1/4)√{(a+b+c)(a+b-c)(c+a-b)(c-a+b)}
=√{2s(2s-2c)(2s-2b)(2s-2a)/16}
=√{s(s-a)(s-b)(s-c)} |
答:672cm2
以上
3.解答例2(Hamayanさん他)
真ん中の三角形GECの面積を求める。
頂点Gから、辺ECに垂線を下ろし、足をHとする。
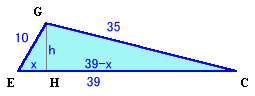
x=EH、h=GHとすると、
x2+h2=102,h2+(39-x)2=352
これより、x = 66/13, h = 112/13を得る。
三角形GECの面積=1/2×39×66/13=168
以下同様。
4.解答例3(Taroさん、M.Hossieさん他)
真ん中の三角形GECの面積を求める。
角EGC=θとする。
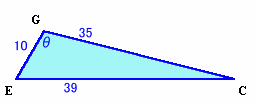
余弦定理より、
cosθ=(102+352−392)/(2・10・35)=−7/25、
sinθ=√(1−(-7/25)2)=√(576/625)=24/25。
よって、三角形GEC=1/2×10・35・sinθ=5・35・24/25=168
以下同様。
4.解答例3(ありっちさん他)
真ん中の三角形の面積を求める。
縦21cm、横36cmの長方形ABCDを考えます。
辺AB上にF、辺AD上にEを下図のようにとる。
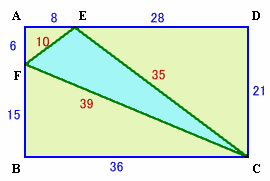
AF=2・3、AE=2・4よりEF=2・5=10。
CD=7・3、ED=7・4よりEC=7・5=35。
BF=3・5、BC=3・12よりCF=3・13=39。
よって、
三角形EFC=36×21−(1/2×6×8+1/2×21×28+1/2×15×36)=168
以下同様。
5.解答例4(イデムリンさん他)
真ん中の三角形の面積を求める。
縦27cm、横36cmの直角三角形ABCを考えます。
辺AB上にD、H、辺AC上にEを下図のようにとる。
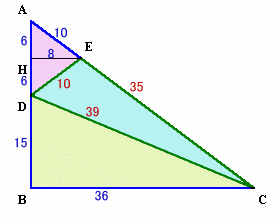
三角形ABCは、9・3、9・4、9・5の直角三角形、EC=45−10=35cm、
AH=2・3、AE=2・5よりEH=2・4=8cm。
よって、三角形DHEも三角形AHE同様、6、8、10の直角三角形、
DE=10cm。
BD=3・5、BC=3・12よりCD=3・13=39cm。
よって、
三角形DEC=1/2×36×27−(1/2×12×8+1/2×15×36)=168
以下同様。





