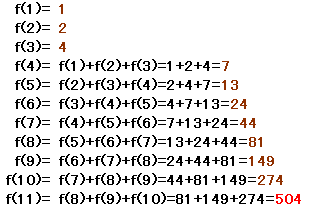第１９６問の解答

---

１．問題　［規則性］

ある長さのひもを、１ｍ・２ｍ・３ｍのひもに分割することを考えます。 例えば、３ｍのひもならば、 １ｍ＋１ｍ＋１ｍ　（左から１ｍの所と２ｍの所で切断） １ｍ＋２ｍ　　　　（左から１ｍの所で切断） ２ｍ＋１ｍ　　　　（左から２ｍの所で切断） ３ｍ　　　　　　　（切断せず） の４通りの分割方法が考えられます。（切る場所が違う場合は「別の方法」であると考えます。） では、１１ｍのひもを切断するとき、何通りの分割方法が考えられるでしょうか。

---

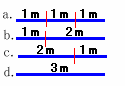２．解答例１
（杉本未来さん、ありっちさん、sambaGREENさん、ヒデー王子さん、あずさ猫さん、ＴＯＲＡさん、
まるけんさん、他多数）

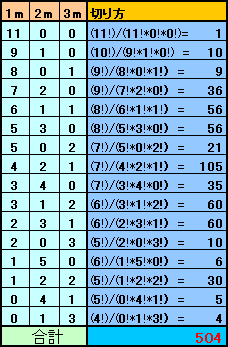
ひもの長さをｎメートルとしたときの、切り方の場合の数をｆ（ｎ）とします。

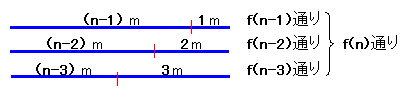
一番右端を何ｍにするかで場合分けします。

• 右端が１ｍのとき：残った左の（n-1)メートルの分割でｆ（ｎ−１）通り 

• 右端が２ｍのとき：残った左の（n-２)メートルの分割でｆ（ｎ−２）通り 

• 右端が３ｍのとき：残った左の（n-３)メートルの分割でｆ（ｎ−３）通り 

従って、ｆ（ｎ）＝ｆ（ｎ−１）＋ｆ（ｎ−２）＋ｆ（ｎ−３）が成り立つ。

f(1)=1,f(2)=2,f(3)=4は明らかだから、これらを使って次々と求めていけばよい。

３．解答例２（Hamayanさん、M.Hossieさん、あやのりんさん他）

１１ｍのひもを１ｍ×ｐ本、２ｍ×ｑ本、３ｍ×ｒ本に切ったとする。

これらを並べ替える場合の数は、（ｐ＋ｑ＋ｒ）！通りある。
このうち、ｐ本の１ｍ、ｑ本の２ｍ、ｒ本の３ｍは同じものなので重複して数えているので、
結局、（ｐ＋ｑ＋ｒ）！／（ｐ！・ｑ！・ｒ！）通りとなる。

１ｍ、２ｍ、３ｍに切る切り方は下表のようになるので、合計５０４通りとなる。