第１９７問の解答

---

１．問題　［平面図形］

左図で、△ＡＢＣは、∠Ａ＝９０°でＡＢ＞ＡＣの直角三角形で、点Ｈは、ＡからＢＣに下ろした垂線の足です。 ＡＢ、ＡＣ上に点Ｐ、Ｑをとり、ＡＰＲＱを１辺がＡＨに等しい正方形とします。 また、△ＳＲＴの周りの長さは１２cmで、正方形ＡＰＲＱの面積は△ＡＢＣと比較すると“△ＡＨＣの面積の４分の１だけ”小さかったそうです。 　では、△ＡＢＣの面積は何cm2でしょうか。

---

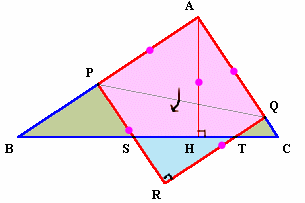２．解答例１（マサルさん、数楽者さん、まるけんさん、うっしーさん、他多数）

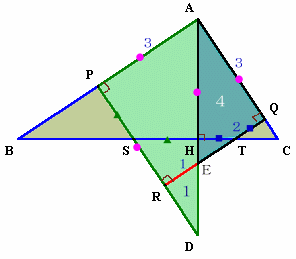
ＰＲ、ＡＨをそれぞれ延長して交わる点をＤとし、ＡＤとＲＱの交点をＥとする。

△ＡＢＨと△ＡＤＰについて、
　ＡＨ＝ＡＰ、∠ＢＡＨ＝∠ＤＡＰ（共通）、∠ＡＨＢ＝∠ＡＰＤ＝９０°
よって、１辺と２挟角が等しいので合同。

すると、△ＢＳＰと△ＤＳＨについて、三角が等しいので相似となり、
　ＢＰ＝ＡＢ−ＡＰ＝ＡＤ−ＡＨ＝ＤＨ
よって、△ＢＳＰと△ＤＳＨは合同。

従って、ＳＰ＝ＳＨ。

同様に、△ＡＣＨと△ＡＥＱは合同、△ＥＴＨと△ＣＴＱは合同、
よって、ＴＨ＝ＴＱ。

　△ＳＲＴの周の長さ
＝ＳＲ＋ＳＴ＋ＴＲ
＝ＳＲ＋（ＳＨ＋ＨＴ）＋ＴＲ
＝（ＳＲ＋ＳＰ）＋（ＴＱ＋ＴＲ）
＝２×ＡＨ
＝１２ｃｍ。

よって、ＡＨ＝６ｃｍ。

さて、△ＡＢＣの面積＝△ＡＢＨ＋△ＡＣＨ＝△ＡＤＰ＋△ＡＥＱ。
よって、△ＥＤＲの面積＝△ＡＣＨ×１/４＝△ＡＥＱ×１/４。

△ＥＤＲと△ＡＥＱは相似なので、面積比が１：４だから辺の比は１：２。
よって、ＲＥ：ＥＱ＝１：２。

従って、ＣＨ：ＡＨ＝ＥＱ：ＲＱ＝２：３。

ＡＨ＝６ｃｍだから、
ＢＨ＝ＡＨ×３/２＝６×３/２＝９ｃｍ、
ＣＨ＝ＡＨ×２/３＝６×２/３＝４ｃｍ、
ＢＣ＝ＢＨ＋ＣＨ＝９＋４＝１３ｃｍ。

よって、△ＡＢＣ＝１/２×ＢＣ×ＡＨ＝１/２×１３×６＝３９ｃｍ²。

３．解答例２（M.Hossieさん、Taroさん、きょえぴさん他）

辺ＡＨ＝ｈ、ＡＣ：ＡＢ：ＢＣ＝１：ｋ：ｔ　とおく。
△ＡＢＨ、△ＡＣＨ、△ＳＲＴは、全て△ＡＢＣと相似。

　ＡＢ＝ＡＨ×ＢＣ/ＡＣ＝ｈ・ｔ、
　ＢＰ＝ＡＢ−ＡＰ＝ｈ・ｔ−ｈ＝ｈ・（ｔ−１）。
　ＰＳ＝ＢＰ×ＡＣ/ＡＢ＝ｈ・（ｔ−１）／ｋ。

よって、ＲＳ＝ＰＲ−ＰＳ＝ｈ−ｈ・（ｔ−１）／ｋ＝ｈ・（ｋ＋１−ｔ）／ｋ。

　△ＳＲＴの周の長さ
＝ＲＳ×（１＋ｋ＋ｔ）
＝ｈ・（ｋ＋１−ｔ）／ｋ×（ｋ＋１＋ｔ）
＝ｈ×（（ｋ＋１）²−ｔ²）／ｋ
＝ｈ×（ｋ²＋２ｋ＋１−ｔ²）／ｋ
＝ｈ×２ｋ／ｋ　（ｔ²＝ｋ²＋１だから）
＝２ｈ＝１２
よって、ｈ＝６ｃｍ。

　△ＡＢＣの面積
＝１/２×（ＢＨ＋ＣＨ）×ＡＨ
＝１/２×（ｈ・ｋ＋ｈ/ｋ）×ｈ
＝１/２×（ｋ²＋１）/ｋ×ｈ²。

　△ＡＣＨの面積
＝１/２×ＣＨ×ＡＨ
＝１/２×１/ｋ×ｈ²。

正方形ＰＱＲＳの面積＝ｈ²。

従って、
　１/２×（ｋ²＋１）/ｋ×ｈ²−１/４×１/２×１/ｋ×ｈ²＝ｈ²、
　４（ｋ²＋１）−１＝８ｋ、
　４ｋ²−８ｋ＋３＝０、
　（２ｋ−３）・（２ｋ−１）＝０、
　ｋ＝３/２、２/３を得る。

ＡＢ＞ＡＣより、ｋ＞１となるので、ｋ＝３/２。

　△ＡＢＣの面積
＝１/２×（ｋ²＋１）/ｋ×ｈ²
＝１/２×（ｋ＋１/ｋ）×６²
＝６／２×（３/２×６＋２/３×６）
＝３×（９＋４）
＝３９ｃｍ²。