第１９８問の解答

---

１．問題　［通過算］

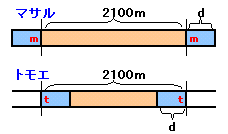
ある電車の先頭にマサルさん、最後尾にトモエさんが乗っており、電車は長さ２１００ｍの橋を渡ろうとしています。 　マサルさんは、電車の先頭が橋を渡り始めると同時に最後尾を目指して歩き始め、電車の最後尾が橋を渡り終えると同時に最後尾に到着しました。 　トモエさんは、電車の最後尾が橋を渡り始めると同時に先頭を目指して歩き始め、電車の先頭が橋を渡り終えると同時に先頭に到着しました。 　マサルさんとトモエさんの歩く速さの比は７：８であったそうです。このとき、 （１）電車の長さは何ｍでしょうか。 （２）電車の速さはマサルさんの歩く速さの何倍でしょうか。

---

２．解答例１（ＴＯＲＡさん、Taroさん、すけべえ￥にーしーむーらーさん、長野美光さん、他多数）

電車の長さをｄmとします。

図１

図２

図１より、
　マサルさんがｄm歩く間に、電車は（２１００＋ｄ）m走り、
　トモエさんがｄm歩く間に、電車は（２１００−ｄ）m走ります。

２人がｄm歩く時間の比は、速度の比と反比例するので、８：７。
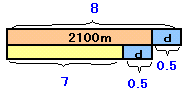
よって、（２１００＋ｄ）：（２１００−ｄ）＝８：７。

図２より、
　２１００：ｄ＝７．５：０．５、
　ｄ＝２１００×０．５／７．５＝２１００／１５＝１４０m

また、電車とマサルさんの速度比は、
　（２１００＋ｄ）：ｄ＝（１５ｄ＋ｄ）：ｄ＝１６：１となります。

答：（１）１４０ｍ、（２）１６倍

　以上

３．解答例２（杉本未来さん、うっしーさん、ありっちさん他）

電車の長さをｄm、速さをｖ１m/s、
マサルさんとトモエさんの速さをｖ２m/s、ｖ３m/sとします。

マサルさんがｄm歩く時間に、電車は（２１００＋ｄ）走るので、
　（2100＋ｄ）／v1＝d／v2　・・・（１） 

トモエさんがｄm歩く時間に、電車は（２１００−ｄ）走るので、
　（ 2100−ｄ）／v1＝d／v３　・・・（１） 

（１）／（２）より、
　（ 2100＋ｄ）／（ 2100−ｄ）＝v３／v2＝８：７
　（ 2100＋ｄ）×７＝（ 2100−ｄ）×８
　2100×７＋７ｄ＝2100×８−８ｄ
　１５ｄ＝2100
よって、ｄ＝2100／１５＝１４０m。

（１）より、
　ｖ１／ｖ２＝（2100＋ｄ）／ｄ＝（１５ｄ＋ｄ）／ｄ＝１６。