第１９９問の解答

---

１．問題　［平面図形］

角Ｃ＝９０度、ＢＣ＝２cmの直角三角形ＡＢＣがあります。 角Ｂの二等分線をひき、辺ＡＣとの交点をＰとすると、ＣＰ＝１cmでした。 では、直角三角形ＡＢＣの面積は何cm2でしょうか。

---

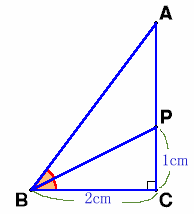２．解答例１（CRYING DOLPHINさん、トトロ@Nさん、うっしーさん、サトラさん、H.Takaiさん、むつこさん、じい３さん、他多数）

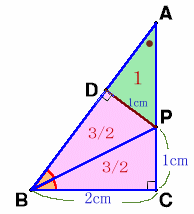
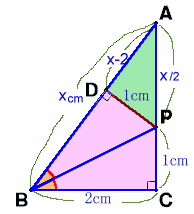
Ｐから辺ＡＢに垂線を下ろし、垂線の足をＤとします。

直角三角形ＰＢＣと直角三角形△ＰＢＤについて、辺ＰＢが共通で∠ＰＢＣ＝∠ＰＢＤより合同。よって、ＰＤ＝ＰＣ＝１ｃｍ。

直角三角形ＡＢＣと直角三角形△ＡＰＤについて、∠ＢＡＣが共通だから相似。相似比は、ＤＰ：ＢＣ＝１：２、よって面積比は１：４。

今、△ＡＰＤの面積を１とすると△ＡＢＣの面積は４、
よって△ＰＢＣ、△ＰＢＤの面積＝（４−１）／２＝３/２。

実際の△ＰＢＣの面積
　＝１/２×ＢＣ×ＰＣ
　＝１/２×２×１
　＝１ｃｍ²。

よって、△ＡＢＣの面積
　＝４／（３/２）×△ＰＢＣ
　＝８/３×１
　＝８/３ｃｍ²

答：８/３ｃｍ²

　以上

---

３．解答例２（萬田銀次郎さん、たなかさん、sambaGREENさん、他）

ＡＢ＝ｘとおきます。

解答例１と同様にして、△ＰＢＤと△ＰＢＣは合同、△ＡＢＣと△ＡＰＤは相似。
よって、ＢＤ＝ＢＣ＝２ｃｍ、ＡＤ＝ＡＢ−ＡＤ＝（ｘ−２）ｃｍ。
ＡＰ＝ＤＰ×（ＡＢ／ＢＣ）＝ｘ／２ｃｍ。

△ＡＰＤは直角三角形だから、ピタゴラスの定理より、
　（ｘ−２）²＋１＝（ｘ／２）²、３ｘ²−１６ｘ＋２０＝０、（３ｘ−１０）（ｘ−２）＝０
　ｘ＝１０/３またはｘ＝２
ＡＤ＝ｘ−２＞０より、ｘ＝２は不適。
よって、ｘ＝１０/３。

△ＡＢＣ＝１/２×ＢＣ×ＰＣ
　　＝１/２×２×（１０/３×１/２＋１）
　　＝８/３ｃｍ²。

　以上

４．解答例３（Taroさん、杉本未来さん、丸天後藤様、AUさん、ＡЯＣさん、Hamayanさん、jackalさん、他多数）

∠ＡＢＰ＝∠ＰＢＣ＝θとおきます。

tanθ＝ＰＣ／ＢＣ＝１/２より、
ＡＣ＝ＢＣ×tan２θ
　　＝２×２tanθ／（１−tan²θ）
　　＝２×２×1/2／（１−(1/2)²）
　　＝８/３

よって、△ＡＢＣの面積
　＝１/２×ＢＣ×ＡＣ
　＝１/２×１×８/３
　＝８/３cm²