第２００問の解答

---

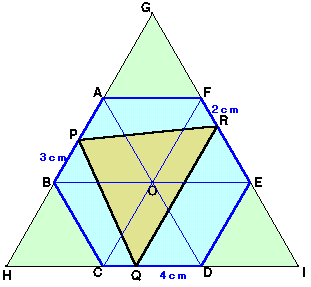
１．問題　［平面図形］

左図のように、正六角形ＡＢＣＤＥＦの内部の点Ｔから辺ＡＢ、辺ＣＤ、辺ＥＦに垂線を降ろし、その足をそれぞれＰ、Ｑ、Ｒとしたところ、ＰＢ＝３cm、ＱＤ＝４cm、ＲＦ＝２cmとなりました。 このとき、黄色の部分（三角形ＰＱＲ）の面積は、水色の部分（正六角形ＡＢＣＤＥＦから三角形ＰＱＲを除いた部分）の面積の何倍でしょうか。

---

２．解答例１（Taroさん、わかさひ君、しゅうさん、長野美光さん、他）

まず、正６角形ＡＢＣＤＥＦの１辺の長さがａ＝６ｃｍと分かっているものとして面積を求めます。
辺ＡＢ、ＣＤ、ＥＦを延長してできる正三角形をＧＨＩとします。

正６角形ＡＢＣＤＥＦの面積＝S0、
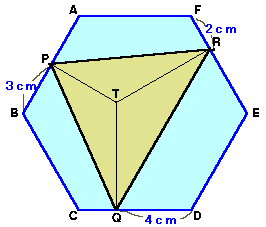
黄色の部分（三角形ＰＱＲ）の面積＝S1、
水色の部分（正六角形ＡＢＣＤＥＦから三角形ＰＱＲを除いた部分）の面積＝S2
とします。
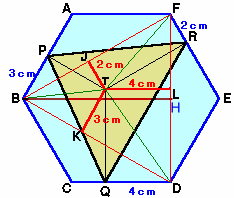
また、１辺が１ｃｍである正三角形の面積を１として以下を計算します。

S21＝△ＡＰＦＲ＝△ＧＢＥ−△ＧＡＦ＝(a+2)(2a-3)-a²＝8×9-6²＝36
S22＝△ＰＢＣＱ＝△ＨＱＰ−△ＨＣＢ＝(a+3)(2a-4)-a²＝9×8-6²＝36
S23＝△ＱＤＥＲＲ＝△ＩＲＱ−△ＩＥＤ＝(a+4)(2a-2)-a²＝10×10-6²＝64
S2＝S21+S22+S33＝36+36+64＝136
S1＝S0-S2＝6a²-136＝6×6²-136＝80
よって、S1／S2＝80/136＝10/17となります。

答：10/17

　以上

---

３．１辺を求める（ヒデー王子さん、まるケンさん、ありっちさん、M.Hossieさん他）

まず、正６角形ＡＢＣＤＥＦの１辺ａが与えられたとき、内部の点Ｔがどこにあっても、ＰＢ＋ＱＤ＋ＲＦは一定の値となることを証明します。

いろいろな証明法があるようですが、ここでは面積を使う方法で説明することにします。

Ｔから正三角形ＢＤＦ(１辺の長さ＝ｂとします)に垂線を下ろし、足をＪ、Ｋ、Ｌとします。
四角形ＪＴＲＦは４つの角が全て９０度なので長方形となり、ＲＦ＝ＴＪとなります。
同様に、四角形ＰＢＫＴは長方形でＰＢ＝ＴＫ、四角形ＴＫＤＲは長方形でＱＤ＝ＴＬとなります。

従って、ＰＢ＋ＱＤ＋ＲＦ＝ＴＫ＋ＴＬ＋ＴＪとなります。

正三角形ＢＤＦの面積＝△ＴＢＤ＋△ＴＤＦ＋△ＴＦＢ
　　＝１/２×ＢＤ×ＴＫ＋１/２×ＤＦ×ＴＬ＋１/２×ＦＢ×ＴＪ
　　＝１/２×ｂ×（ＴＫ＋ＴＬ＋ＴＪ）　・・（１）
　　＝１/２×ＦＤ×ＢＨ
　　＝１/２×ｂ×３/２×ａ　　・・（２）

よって、（１）、（２）より、ＴＫ＋ＴＬ＋ＴＪ＝３/２×ａ、
従って、ＰＢ＋ＱＤ＋ＲＦ＝３/２×ａとなり、Ｔの位置に係わらず一定値となることが分かります。

よって、３＋４＋２＝３/２×ａ、ａ＝９×２/３＝６ｃｍとなります。

　以上