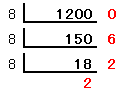第3問の解答
問題 [整数の性質]
|
|
|
|
|
|
あるパチンコ屋さんが開店しました。パチンコ台の設置台数が1200台というマンモス店です。 そこで、店長さんはパチンコ台に1台1台番号をつけることにしました。 1台目は1番、2台目は2番、という具合に番号をつけるのですが、ただし4と9は縁起が悪いので使いません。 |
|
|
|
|
|
解答例(マサルさん)
8進法を利用して解く問題です。
8進法というのは、(コンピューターに詳しい方ならご存じと思いますが)数の数え方の一種です。
例えば、私たちが普段使っている数は10進法ですが、これは数が10個増えるごとに位上げが行われる数です。8進法はその名の通り、数が8個増えるごとに位上げが行われる数です。
例えば10進法は
1、2、3、4、5、6、7、8、9、10、11、12....のように数が進みます。
これに対して8進法は
1、2、3、4、5、6、7、10、11、12....のように進むのです。
この問題は、4と9を使わずに台番号を表記しますから、いわば変則8進法の問題です。つまり、
となっているわけです。このことに注目すると、楽に問題を扱うことができます。
(とはいってもかなり難しいですが)
問1:台番号が217番のパチンコ台は何台目の台でしょうか。
変則8進法の217は、普通の8進法では216となります。
ここまできたら、あとは8進数を10進数に直せばよいだけです。
#ここで、8進数を10進数に直す方法を伝授しましょう。
まずは、10進数のしくみから。
10進数で125といえば、100が1個、10が2個、1が5個集まっていることを表していますね。
これはまさに10進法が10進むと1つ位上げが行われるからです。
つまり、1の位の数が10増えると、10の位は1増えます。
つまり、10の位は1の位10個分の役割をしているのです。
同様に、8進数で216といえば、64(8*8)が2個、8が1個、1が6個集まってできた数です。
ですから8進数の216を10進数に直すと、
64*2+8*1+1*6=142
答:(1) 142番目
問2:この店の最後のパチンコ台は何番台でしょう?
今度は逆に10進数を8進数に直せばよいのです。
1200という10進数を8進数に直してみます。これには、ある計算方法を用いるとよいのですが 今回は理解しやすいように手動で(?)やってみることにします。
まず、1200が何桁の数か分からないので、検討をつけて計算してみることにします。
ま、1200でしたらおそらく4桁であろうことは容易に想像がつくので、ここでは(右からから数えて)4桁目から計算します。
8進法で右から4桁目は、1つの数が8*8*8=512を表しています。
そこで、1200の中に512がいくつ含まれるかを計算します。
1200÷512=2あまり176
これで、右から4桁目は2であることがわかりました。
次は右から3桁目です。右から3桁目は8*8=64を表しています。
そこで、余った176の中に64がいくつあるかを調べます。
176÷64=2あまり48
これで、右から4桁目も2であることがわかりました。
同様に、2桁目を
48÷8=6あまり0
とし、1桁目は2桁目を出した時点であまりがないので0とします。
すると、10進法で1200と表された数は、8進法では2260となることがわかります。もう一つの方法は、下図のように10進数を8で次々に割って余りを右に書き出します。
余りを逆に並べると8進数になっています。この例ですと、2260ですね。
で、ここで答えを2260とすると間違いで、問題はパチンコ台ですから変則8進法になおさねばなりません。
普通の8進法で2260であれば、変則8進法では2270となりますから、答えは2270番台、ということになります。
答:(2) 2270番台以上