第6問の解答
問題 [空間図形]
|
|
|
|
|
|
|
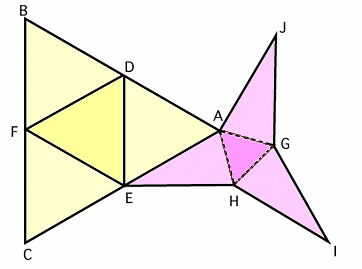 |
左図は、ある立体の展開図です。 AD、DB、....などの実線で示された辺は6cm、 このとき、この立体の体積を求めなさい。
|
|
|
|
|
|
|
解答例(マサルさん)
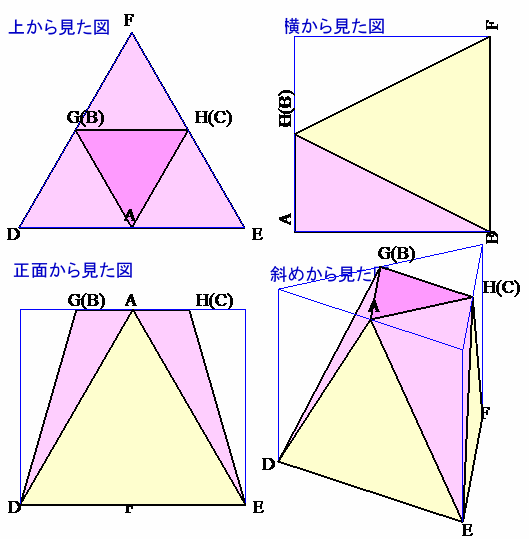
問題の展開図を組み立てると、下の図のようになります。
(参考)マウスでドラッグして下さい。
この立体は、側面の3つの正三角形が底面に対して垂直に立っていることが分かります。
従って、一辺の長さが6cmの正三角形の高さがこの立体の高さであることが分かります。
正三角形の面積=1/2×6×高さ≒15cm2 より、
正三角形の面積=15×2/6≒5cm。さらに、見取り図をよく見ると、この立体は三角柱から三角錐を3つ切り取ってできたものであることが分かります。
これらの三角錐は、三角柱と比べると底面が1/4で、さらに角錐であることから1/3の体積になっています。
従って、
三角柱の体積=底面積×高さ=15×5=75cm3
三角錐の体積=三角錐の体積×1/4×1/3=25/4cm3
よって、求める立体の体積
=75−25/4×3=225/4cm3答: 225/4cm3
以上