第８問の解答

問題　［ 平面図形］

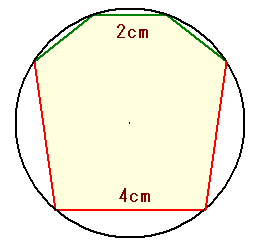問題図 左図は、長さがそれぞれ４cm（赤）、２cm（緑）の６本の棒が円にちょうどすっぽり入ったところを示しています。

このとき、緑の棒と赤の棒で囲まれた６角形の面積を求めなさい。
ただし、１辺の長さが１の正三角形の面積を０.４３cm2とします。

　

解答例（マサルさん）

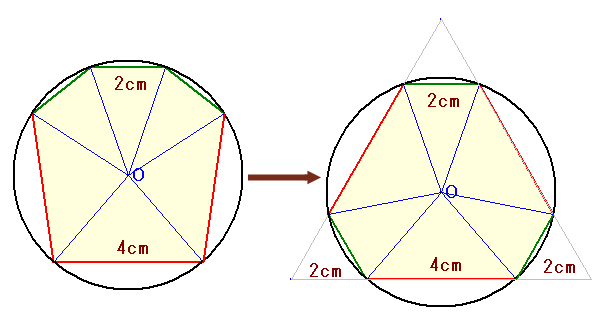
下の図のように、赤の棒と緑の棒を組み替えると、
六角形の各頂点と中心を結ぶと、棒の入れ替えを行っても面積は変わらないことが分かります。

参考図１

右の図をよく見ると、一辺が２＋４＋２＝８cmの正三角形が浮かびあがってきます。
外にはみ出ている三角形は１辺が２cmの正三角形です。

このことから、円の中にできた六角形は１辺２cmの正三角形16-3＝13個分の面積を持っていることが分かります。

では、計算してみましょう。
一辺が２cmの正三角形の面積＝０．４３×４≒１．７２cm2

よって、円の中の六角形の面積≒１．７２×１３＝２２．３６cm2


答：　２２．３６cm2

以上