第９問の解答

問題　［整数の性質］

１番から２０００番までの番号のついたランプがあります。
これらのランプにはそれぞれスイッチがついており、
押すたびごとに、ランプが点灯⇔消灯を繰り返します。

現在、全てのランプが消えている状態で、これから、次のような作業を行います。

  1. 1の倍数のスイッチを押す。
  2. 2の倍数のスイッチを押す。
  3. 3の倍数のスイッチを押す。
  4. 4の倍数のスイッチを押す。
    　　　　　　・
    　　　　　　・
  5. 2000の倍数のスイッチを押す。

１.〜２０００.の作業を終えたとき、点灯しているランプは（　）個でした。

（　）にあてはまる数を求めなさい。

解答例（マサルさん）

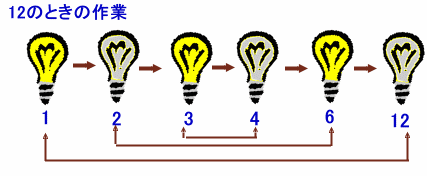
例えば、１２番のランプについて考えます。
このランプのスイッチが押されるのは、１２の約数である１、２、３、４、６、１２の各作業を行ったときです。
ということは、

参考図１

となって、結局最後には消えていることになります。

　このことから分かるのは、

  • スイッチは、その番号の約数の作業のときに押される。

  • 約数が偶数個あるときには、消灯した状態で終わる。

ということです。

そこで、”約数の個数”について考えてみると、例えば１２の約数は６個です。
この数え方は、上図のようにすると漏れがありません。

つまり、ある約数に対してかならず「掛けて１２」となる相手を探してやるわけです。
すると、全ての数は約数が偶数個であるかと思われますが、実は例外があるのです。
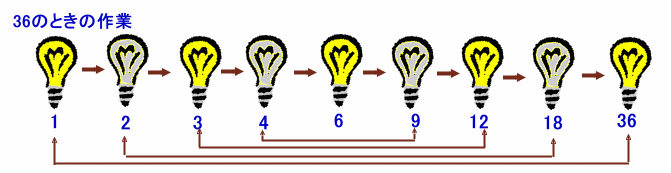
それは....。

（例）３６（約数は９個）

参考図２

上の例のように、真ん中の数が ６×６＝３６のようになる場合、当然約数は奇数個になります。
つまり、同じ数を２回掛けてできた数の約数は奇数個であることがわかります。

解答ですが、このような数が２０００番までに何個あるかを調べればよいことになります。

ここで、
　４３×４３＝１８４９、４４×４４＝１９３６、４５×４５＝２０２５
ですから、1×1〜４４×４４がこの条件にあてはまることになります。

答：　４４個

以上