第２０問の解答

問題　［整数の性質］

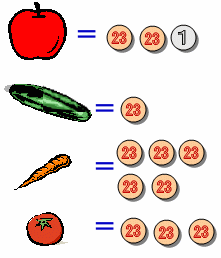
太郎君が、ある日お母さんに買い物を頼まれました。

「ここに３７２０円あるから、これを使ってニンジンとキュウリとトマトとリンゴを買ってきてね。
でも、３７２０円ぴったり使うようにすること。
ぴったりだったら、１つも買わないものがあってもいいわよ。」

さて、太郎君が八百屋さんに行ってみると値段は次のようになっていました。

  • ニンジン・・・・・１本１１５円
  • キュウリ・・・・・１本　２３円
  • トマト　　・・・・・１個　９２円
  • リンゴ　・・・・・・１個　４７円

さて、ここで太郎君は考えて見事ちょうど３７２０円で買うことに成功したそうです。
さて、太郎君はリンゴを何個買ったと考えられますか。考えられる数を全て答えてください。

解答例１（マサルさん）

ニンジン、キュウリ、トマトの金額は全て２３の倍数になっています。
そしてリンゴは４７円ということですから、２３で割ると１余る数です。

参考図１

このことから、

  • リンゴを１個も買わなければ全体の金額は２３で割り切れる。

  • そして、リンゴを１個買うごとに１円ずつ余りが生ずる。

ということが分かります。

参考図２

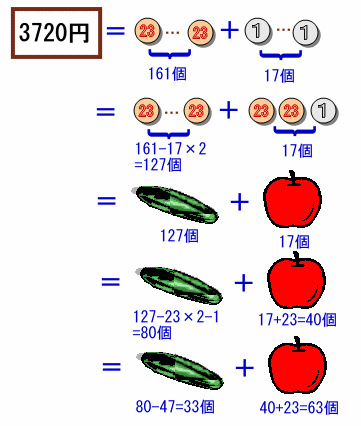
というわけで、３２７０＝２３×１６１＋１７ですから、まずは１７個が解答の１つです。

さらに、リンゴをあと２３個買うと余りは４０円となり、この余りを使ってキュウリを１本買うとぴったりになりますから、４０個も正解であると分かります。

同様にして、６３個も正解であることが分かります。

答：　１７個、４０個、６３個

以上

（参考）式で考える

上記より、リンゴとキュウリのみ考えれば良いことになります。
そこで、リンゴをn個、キュウリをm個買うことにします。

　４７n＋２３m＝３７２０
　（２３×２＋１）n＋２３m＝２３×１６１＋１７
　n−１７＝２３×（１６１−２ｎ−m）

よって、n−１７は２３の倍数となるので、n＝２３×p＋１７と書けます。
このとき、m＝１２７−４７×ｐ

n、m≧0の条件を満たすには、１≦p≦３のときなので、n＝１７、４０、６０が解となります。