第２５問の解答

問題　［平面図形］

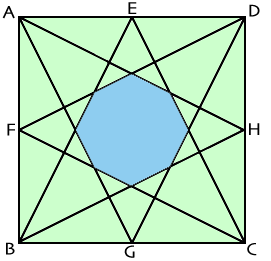問題図 左図で、四角形ＡＢＣＤは１辺の長さが６cmの正方形、
点Ｅ、Ｆ、Ｇ、Ｈはそれぞれ各辺の中点です。

このとき、内部にできた水色の部分の面積を求めなさい。

解答例１（マサルさん）

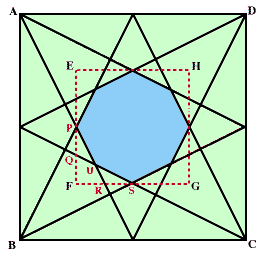
下の図のように、水色の部分の周りに正方形ＥＦＧＨを設定します。

参考図１

この中にできた八角形（正八角形ではありません）の面積を求めればよいことになります。
ここで、点Ｑ、ＲはそれぞれＰＦ、ＦＳの中点です。

すると、ＱＰ：ＰＳ＝１：２であることが分かりますから、
　△ＰＳＵ＝△ＰＦＳ×１/３
であることになります。

すると....。水色の部分の面積は四角形ＥＦＧＨの
　　１/２＋１/８×１/３×４＝２/３
であることが分かります。

正方形ＥＦＧＨ
　＝正方形ＡＢＣＤ×１/４
　＝３６×１／４×２／３＝６cm2
と分かります。
　　　　　　　　　　　　

答：　６ｃｍ2

以上

解答例２（マサルさん）

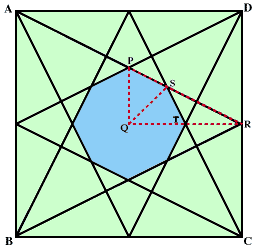
下の図のような△ＰＱＲを考えます。

参考図２

すると、△ＰＱＳと△ＴＱＳは合同ですから、面積は当然等しくなっています。

また、ＱＴ：ＴＲ＝１：１ですから、△ＳＱＴと△ＳＴＲの面積も等しいことが分かります。
つまり、△ＰＱＳ＝△ＳＱＴ＝△ＳＴＲとなります。

ここで、△ＰＱＳ＝３６×１/１６＝９/４cm2
となりますから、

水色の部分の面積＝９/４×２/３×４＝６cm2
と分かります。