第27問の解答
問題 [空間図形]
|
|
|
|
|
|
|
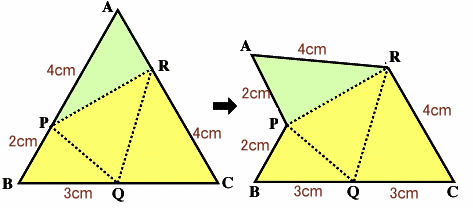 |
左図のような正三角形ABCがあります。 この三角形を点線で折り、さらに△APRをひっくり返してつなぎ合わせたものが右側の図です。 このとき、この図を組み立てるとある立体が完成します。 |
|
|
|
|
|
|
解答例1(マサルさん)
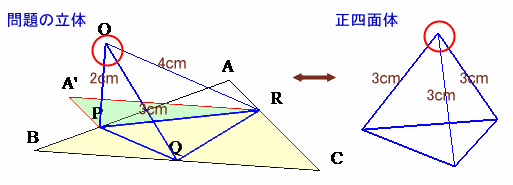
下図をご覧ください。左は問題で与えられた立体の図、右は正四面体です。
この2つをよく比べると、赤く囲った部分はいずれも60度の角度が集まってできています。
つまり、左側の立体を右側の立体にかぶせると、この部分はぴったり重なるんですね。
こうなると、あとは底面積と高さを比較すればよいことになります。
ここで、底面のとり方がポイントになります。上の図のままだと2つが重なることを発見した意味がありません。
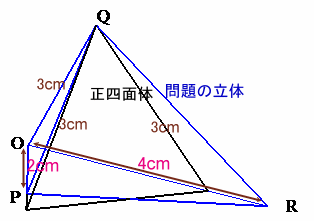
ここでは、上の図で見ると側面にあたる△OPRを底面とします。(要するに、横に倒します。)
すると、下図のように、高さを共通にすることができます。
(参考)マウスでドラッグして下さい。
こうなれば、底面積を比べるだけです。
というわけで、求める体積比=底面積の比=4/3×2/3=8/9と分かります。答: 8/9倍
以上