第３１問の解答

問題　［平面図形］

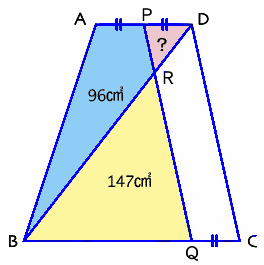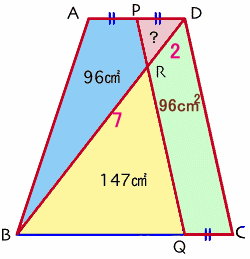
問題図 左図で、四角形ＡＢＣＤは、辺ＡＤと辺ＢＣが平行な台形です。
また、ＡＰ＝ＰＤ＝ＱＣです。

四角形ＡＢＲＰの面積が９６cm2、△ＢＱＲの面積が１４７cm2であるとき、△ＰＲＤの面積を求めて下さい。

解答例１（マサルさん）

参考図１

△ＡＢＤと平行四辺形ＰＱＣＤの面積を比較してみます。
△ＡＢＤ＝AD×高さ÷２、平行四辺形ＰＱＣＤ＝PD×高さで、
AD＝２×PDより、△ＡＢＤ＝平行四辺形ＰＱＣＤ。

従って、重なった部分△PDRを除くと、
　四角形ＲＱＣＤ＝四角形ABRP＝９６cm2。

△ＢＱＲと△ＢＣＤは相似で、
面積比は１４７：(１４７＋９６)＝４９：８１＝７2：９2と分かります。
よって、相似比は７：９ですね。

従って、ＢＲ：ＲＤ＝７：２であることが分かります。

△ＢＲＱと△ＤＲＰは相似ですから、その面積比は７2：２2＝４９：４。
従って、求める面積＝１４７×４／４９＝１２cm2と分かります。

答：　１２cm2

以上