第３２問の解答

問題　［場合の数］

足のなが〜い太郎君は、階段を１段ずつ、２段ずつ、３段ずつの３通りで上ることができます。

このとき、例えば全３段の階段を上るとすると、太郎君は、
  • １段＋１段＋１段
  • １段＋２段
  • ２段＋１段
  • ３段

の４通りの上り方をすることができます。

では、全１２段の階段を上るとき、太郎君は何通りの上り方をすることができるでしょうか。

解答例１（マサルさん）

参考図１

この問題は数列で考える問題です。（フィボナッチ数列といいます。）

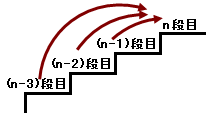
太郎君は１段、２段、３段の３通りの上り方ができます。

n番目の階段にいるとき＝
　　（n-1）番目から上がる場合＋（n−2）番目から上がる場合
　＋（n-3）番目から上がる場合。

  1. 階段が１段　・・・　１通り。

  2. 階段が２段だった場合。１段目から上がる場合が１通り。
    　　　　　　　　　　　　　　　０段目から上がる場合が１通り。
    　　　　　　　　　　　　　　　合計２通りです。

  3. 階段が３段だった場合。２段目から上がる場合が２通り。
    　　　　　　　　　　　　　　　１段目から上がる場合が１通り。
    　　　　　　　　　　　　　　　０段目から上がる場合が１通り。
    　　　　　　　　　　　　　　　合計４通りですね。

  4. 階段が４段だった場合。３段目から上がる場合が４通り。
    　　　　　　　　　　　　　　　２段目から上がる場合が２通り。
    　　　　　　　　　　　　　　　１段目から上がる場合が１通り。
    　　　　　　　　　　　　　　　合計７通り。

  5. 階段が５段だった場合。４段目から上がる場合が７通り。
    　　　　　　　　　　　　　　　３段目から上がる場合が４通り。
    　　　　　　　　　　　　　　　２段目から上がる場合が２通り。
    　　　　　　　　　　　　　　　合計１３通り。

このようにして、１２段まで計算を続けると.....。

参考図２

答：　９２７通り

以上