第35問の解答
問題 [流水算の問題]
|
|
|
|
|
|
ある上りのエスカレーターがあります。
このエスカレーターは何段あるでしょうか。 |
|
|
|
|
|
解答例1(マサルさん)
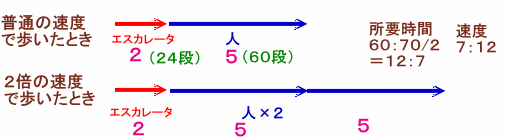
普通に歩いたときと、2倍の速さで歩いたときの所用時間の比を考えます。
すると、60:70÷2=60:35となります。
2倍の速さで歩いた場合は、70段進んでも普通の場合の倍の速さで進んでいますから、時間比はこのようなになります。
さて、ここから両者の速さ比を導きます。ここでいう速さは、「エレベータの速さ+歩く速さ」です。
速さ比は、所用時間の比の逆ですから、
35:60=7:12ということになります。
ここで、両者の速さの差に注目! 5の差がありますね。これが、歩く速さ(普通)です。
すると、エレベータの速さは、7−5=2ということになりますね。
普通に歩いた場合を考えてみましょう。
人が歩いたのは60段です。このとき、エレベータが上らせてくれたのは何段でしょうか...。
先ほどの比から、歩く速さ(普通):エレベータの速さ=5:2ということが分かっています。
これを利用して、
60×2/5=24段
これが、エレベータが上らせてくれた段数です。
よって、エレベータの段数=60+24=84段となります。答: 84段
以上