第３７問の解答

問題　［平面図形］

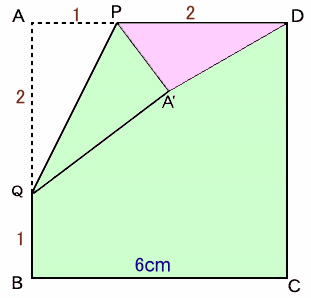問題図 左図は１辺の長さが６cmの正方形ＡＢＣＤを線分ＰＱで折り返したところを示しています。

ＢＱ：ＱＡ＝ＡＰ：ＰＤ＝１：２のとき、△ＰＤＡ’の面積を求めてください。

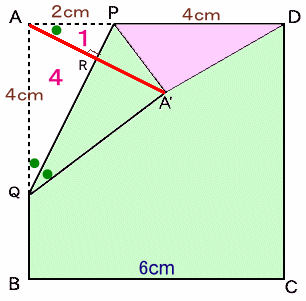
解答例１（マサルさん）

下図のような補助線ＡＡ’を考えます。また、ＡＡ’とＰＱとの交点をＲとします。

参考図１



すると、ＰＱとＡＡ’は垂直に交わることが分かりますね。

ここで、△ＡＰＱ、△ＲＰＡ、△ＲＡＱはそれぞれ相似な関係にあります。
（一つの角度が９０度、もう一つは共通ですから...。）

さて、△ＲＰＡと△ＲＡＱの相似比は１：２です。
ということは、面積比は１：４ということになります。あとはこれを利用して...。

　△ＡＱＰ＝４×２÷２＝４cm2
　△ＲＰＡ＝４×１/５＝０.８cm2
　△ＡＡ’Ｐ＝０.８×２＝１.６cm2

ＡＰ：ＰＤ＝１：２ですから、
　△ＡＡ’Ｐ：△ＰＤＡ’＝１：２　であることが分かります。

従って、
　△ＰＤＡ’＝１.６×２＝３.２cm2となります。
　

答：　３．２cm2

以上