第38問の解答
問題 [ 空間図形]
|
|
|
|
|
|
|
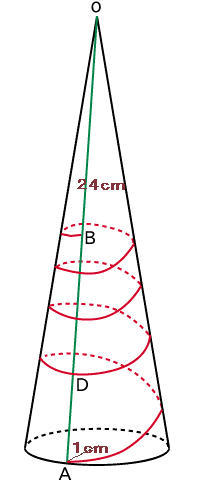 |
左図のような円錐があります。 底面の半径は1cm、OAの長さは24cmです。 この円錐に、図のようにAからOA上の点Bまで、糸をたるまないように4回巻きつけます。 また点Bは、糸の長さが最も短くなるように定めます。 糸がOAと初めに交わる点をDとするとき、ODを一辺とする正方形の面積を求めてください。 |
|
|
|
|
|
|
解答例1(マサルさん)
まずは、この円錐の側面の展開図を考えましょう。側面の形は扇形ですね。
底面の半径は1cmですから、その周の長さは2×3.14cmです。
また、扇形の半径は24cmです。これがもし扇形でなく円だったら48×3.14cmになってしまいます。
ということは、扇形の弧の長さは円である場合の48分の2、つまり24分の1であることが分かります。
そこで、扇形の中心角=360゜×1/24=15゜であることになります。
さてこの扇形に糸を巻きつけるわけですが、4回まきつけるということは、中心角15゜の扇形を4つ並べた平面図を考えれば良いことになります。(下の図参照)
すると、中心角は15゜×4=60゜となります。60゜とくればピンと来ますね?
そう、正三角形です。図の青い点線の△OAA''''は、正三角形です。
さて、ABの長さは考えられる限り最短でなくてはなりません。
これはABがOA''''に垂直に交わるようにすれば良いことになります。
というわけで、この問題で巻いた糸は図の赤線のようになっていることが分かります。あとは、ODを一辺とする正方形の面積です。
ODの長さは中学生以上なら三平方の定理で一発なのですが、小学生はそうはいきません。注目する点は、△ODBが直角二等辺三角形であることです。
ということは、この三角形4つ分でちょうど求める正方形ということになります。OBはOAの中点ですから、OB=12cm。
△ODBの面積=12×12÷2=72cm2です。従って、求める正方形の面積=72×4=288cm2となります。
答: 288cm2
以上