第40問の解答
問題 [平面図形]
|
|
|
|
|
|
|
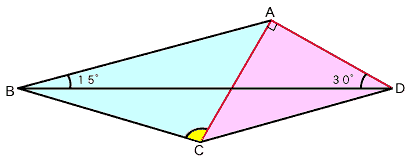 |
左図で、△ACDはAC=ADの直角二等辺三角形です。 また、∠ADB=30゜、∠ABD=15゜です。 このとき、∠ACBの大きさを求めてください。 |
|
|
|
|
|
|
解答例1(マサルさん)
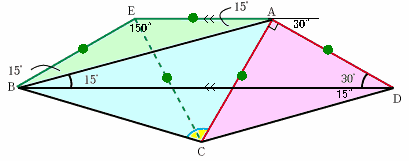
下図をご覧ください。緑色の線が、この問題を解くうえで必要となる補助線です。
ちょっと?強引ですが...。
緑色の補助線は、頂点Aからは辺BDに平行な直線をひき、頂点Bからは∠DBE(Eは前述の平行線上の点)=30゜となるように 引いたものです。すると、四角形EBDAは等脚台形であることから、BE=ADとなります。
また、△EBAは二等辺三角形ですから、BE=EAですね。さらに、△ACDはAC=ADの直角二等辺三角形でしたね。
このことから、AC=EAであることが分かります。
また、∠EAC=∠EAD−∠CAD=150−90=60゜ですね。というわけで、△ECAは正三角形です。
これで、∠ECA=60゜であることが分かりますね。さらに、∠BEC=∠BEA−∠AEC=150−60=90゜であることから、
△BECは直角二等辺三角形です。
というわけで、∠BCE=45゜。
よって∠ACB=60゜+45゜=105゜ となります。答: 105°
以上