第４１問の解答

問題　［平面図形］

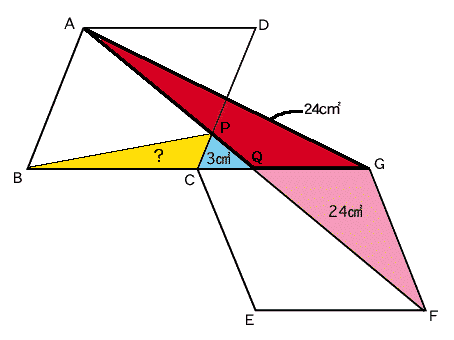
問題図 左図で、四角形ＡＢＣＤと四角形ＥＣＧＦは合同な平行四辺形です。

また、Ｂ、Ｃ、Ｇは一直線上にあります。

△ＰＱＣの面積が３cm2、△ＱＧＦの面積が２４cm2であるとき、△ＰＣＢ（黄色の三角形）の面積を求めて下さい。

解答例１（マサルさん）

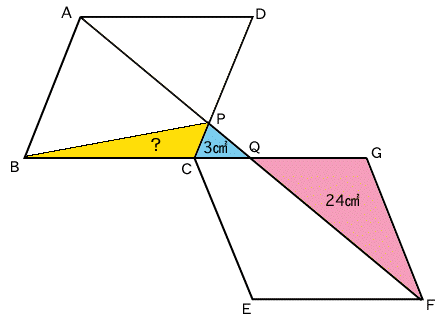
まずは、下図をご覧ください。

参考図１

３直線ＡＤ、ＢＱ、ＥＦはそれぞれ平行で、その間隔も等しくなっていますね。
このことから、ＡＱ＝ＱＦであることが分かります。

すると、△ＡＱＧ＝△ＱＧＦ＝２４cm2であることが分かります。

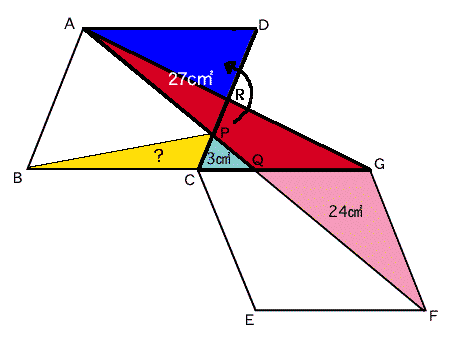
次は下の図です。

参考図２

今度は、ＡＤとＣＧの長さが等しいことを利用しての等積移動です。

△ＡＤＲと△ＧＣＲは合同ですから、当然面積も等しくなっています。
これを利用すると、
△ＡＰＤ＝△APR＋△ADR＝△APR＋△GCR＝△AQG+△PQC＝２４＋２３＝２７cm2と分かります。

すると、△ＡＰＤと△ＱＰＣは相似で、面積比は２７：３＝９：１ですから相似比は３：１です。
つまり、BC：CQ＝AＤ：CQ＝３：１です。

あとは簡単ですね。
求める△ＰＣＢの面積＝△ＡＰＤ×１/３＝２７×１/３＝９cm2 となります。

答：　９cm2

以上