第44問の解答
問題 [ 整数の性質]
|
|
|
|
|
|
算チャレ共和国は変な国で、流通している貨幣は17円玉と18円玉だけであるそうです。 このとき、ぴったりで払うことのできない金額のうち、最大の金額を求めてください。 |
|
|
|
|
|
解答例1
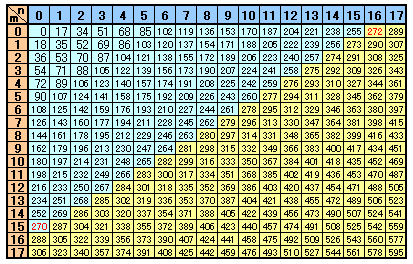
17円玉をn枚と18円玉をm枚で払える額を、0≦n、m≦17の範囲で計算してみます。
272円以上なら、ぴったり払うようなn、mの組み合わせがありそうですが、271円ではなさそうです。
従って、271円 が最大金額のようです。式で確かめてましょう。
N円を17円玉をn枚と18円玉をm枚で払えるとき、
N=17n+18m
が成り立ちます。Nを17で割ったときの商をp、余りをrとすると、
N=17p+r=17(n+m)+mよって、
17(n+m−p)=r−m ・・・ (1)従って、
n+m−p=0、r−m=0 ・・・ (2)
なら(1)が成り立ちます。(2)をn、mについて解くと、
n=p−r、m=r ・・・ (3)
を得ます。もし、N≧272=17×16のとき、p≧16。
rはNを17で割った余りなので、r≦16。よって、(3)を満たすn、mは0≦n、mを満たします。
従って、272円以上なら必ずぴったり支払うことができることが分かります。 ・・・ (4)さて、N=271円がぴったり支払うことができたとします。
271=17×15+16だから、(1)より、
17(n+m−15)=16−m ・・・ (1)’271=17n+18m≧18m、
よって、m≦288/18≒15.05・・
従って、m<16となり、0<16−m≦16。これは、(1)’と矛盾します。
よって、271円をぴったり支払うことはできません。
(4)と合わせて考えれば、271円がぴったり支払えない最大金額と分かります。答: 271円
以上