第45問の解答
問題 [ 空間図形]
|
|
|
|
|
|
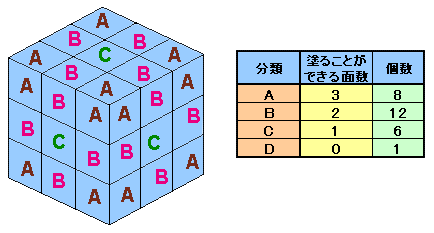
1辺の長さが1cmの立方体が27個あります。 この立方体を組み合わせて1辺の長さが3cmの立方体を作って周りをペンキで塗り、乾いたらバラバラにします。 同様の作業をあと2回繰り返したところ、もとの1辺の長さが1cmの立方体の全ての面がペンキで塗られたそうです。 3回の作業で使ったペンキの色がそれぞれ違うとすると、それぞれの色が2面ずつ塗られている立方体はいくつあるでしょうか。 |
|
|
|
|
|
解答例1
27個の立方体で3cmの立方体を作ったとき、1回の作業でそれぞれ何面をペンキで塗ることができるかで分類してみましょう。
1回の作業で延べ9×6=54面、3回の作業では54×3=162面を塗ることができます。
ところが、27個の立方体には合計6×27=162面あるので、重複して塗るような面はありませんし、
また、どの立方体とも、3回の作業でちょうど6面を塗らなくてはいけません。従って、ある回にDであった立方体は、残りの2回はAでなくてはいけません。
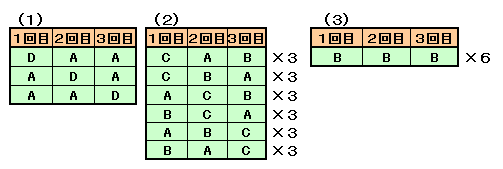
(D:0面、A:3面、A:3面) ・・・ (1)
Dは各回1個ですから、このタイプは延べ3個また、ある回にCであった立方体は、残りの2回はAとBでなくてはいけません。
(C:0面、A:3面、B:2面) ・・・ (2)
Cは各回6個ですから、このタイプは延べ18個(1)と(2)で、各分類の延べ個数を数えてみると、
A:2×3+1×18=24個
B:0×3+1×18=18個
C:0×3+1×18=18個
D:1×3+0×18= 3個
となり、B以外は全て出尽くしています。従って、残り27−3−18=6個は、3回ともBのものとなります。
(B:2面、B:2面、B:2面) ・・・ (3)
求める立方体は、(3)のタイプのものですから、6個あることが分かります。
答: 6個
以上