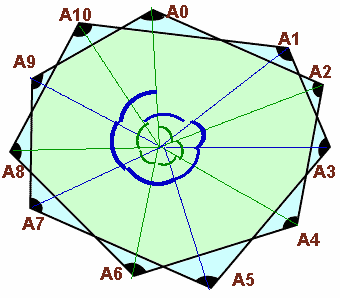
第46問の解答
問題 [ 平面図形]
|
|
|
|
|
|
|
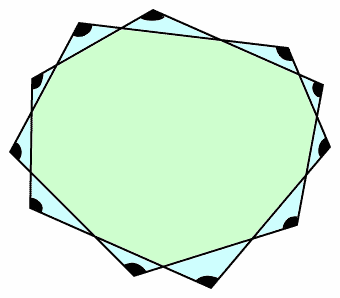 |
左図で、印を付けた部分(黒い部分・計11ヶ所)の角度の和を求めてください。 |
|
|
|
|
|
|
解答例1
各点は、A0→A2→A4→A6→A8→A10→A1→A3→A5→A7→A9→A0
のように2周するので、内側の角度の和=360度×2。よって、求める和は、
Σ(180−内側の角)=180×11−Σ(内側の角)=180×11−360×2=1260度となります。答: 1260度
以上