第４８問の解答

問題　［平面図形］

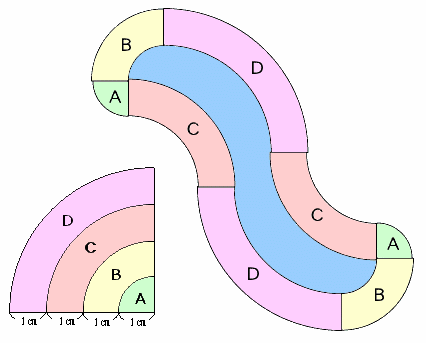問題図 左図のように、半径４cm、中心角９０゜の扇形の紙をＡ〜Ｄに分け、それを並べて右のような図形を作りました。

水色の部分（中にできた部分）の面積を求めてください。ただし、円周率は３.１４とします。

解答例１

マサルさん

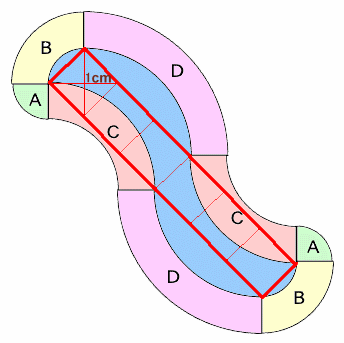
下図のような補助線を考えて、大きめの弓形はそれぞれ等積移動すると、
求める面積は「赤の太線でひいた長方形の面積＋残った弓形２つ」ということになります。

参考図１

長方形は、６つの正方形に分割することができます。

これらの正方形は対角線の長さが２cmの正方形なので、
　面積＝２×２×1/2＝２cm2と分かります。

弓形の面積＝１×１×３.１４×1/4−１×１×1/2＝０．２８５cm2。

従って、求める部分の面積＝２×６＋０．２８５×２＝１２.５７cm2となります。
　

答：　１２.５７cm2

以上