第49問の解答
問題 [平面図形]
|
|
|
|
|
|
|
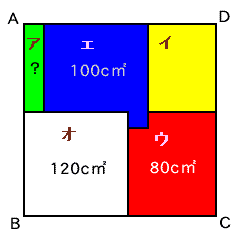 |
左図は、同じ大きさの正方形の折り紙を下から緑色(ア)、黄色(イ)、赤色(ウ)、青色(エ)、白色(オ)の順に重ねて、より大きな正方形ABCDを作ったものです。 上から見ると、白色の部分は120cm2、青色の部分は100cm2、赤色の部分は80cm2となりました。 このとき、緑色の部分の面積を求めてください。 |
|
|
|
|
|
|
解答例1
マサルさん
元の正方形の1辺の長さをa、正方形ABCDの1辺の長さをbとします。
赤い折り紙も青い折り紙も元は正方形ですから、PS=EC=a、また、GC=SR=b−a。
従って、長方形PQRSとFGCEは合同となり、面積も等しくなります。
2つの長方形は合計100+80=180cm2ですから、1つ分はその半分の90cm2です。
よって、青い長方形のでっぱりの部分(カ)=100−90=10cm2と分かります。次に図2で、AT=PS=aより、AP=TS=a−PT、
従って、長方形AUQP=長方形TFRS。さて、BG:GC=長方形UBGF:長方形FGCE=120:90=4:3。
従って、RS=GC=a×3/4。よって、
水色の部分(キ):でっぱりの部分(カ)=a×3/4:a×(1−3/4)=3:1。従って、
求める面積(ア)=水色の部分(キ)=でっぱりの部分(カ)×3=30cm2
となります。
答: 30cm2
以上