第53問の解答
問題 [空間図形 、場合の数]
|
|
|
|
|
|
|
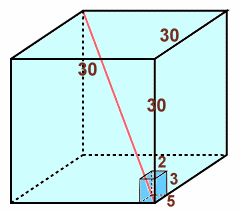 |
3つの辺の長さが2cm、3cm、5cmの直方体がたくさんあります。 この直方体を同じ向きにすきまなく並べたり重ねたりして、一辺の長さが30cmの大きな立方体を作ります。 このとき、大きい立方体の1つの対角線は、何個の小さい直方体を貫通するでしょうか。 |
|
|
|
|
|
|
解答例1
マサルさん
まずは平面図形で考えてみましょう。
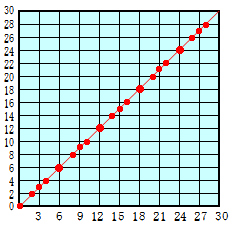
図は、縦2cm、横3cmの長方形を同じ向きにならべて一辺が30cmの正方形を作り、対角線をひいたところを示しています。
この対角線がいくつの長方形を横切っているかを数えると20個になります。
対角線が新しい長方形を通過するときを、長方形の左または下の辺と対角線が交わるときと考えます。
対角線の座標は(t,t)(ただし、0≦t<30)で表されますから、tが2または3の倍数のときの個数を数えれば良いことになります。従って、通過する長方形の個数
=2の倍数+3の倍数−6の倍数
=30/2+30/3−30/6=15+10−5=20個
となります。立体の場合も全く同様です。
対角線の座標は、(t,t,t)(ただし、0≦t<30)で表されますから、tが2または 3または5の倍数のときの個数を数えれば良いことになります。
従って、通過する直方体の個数
=2の倍数+3の倍数+5の倍数−(6の倍数+10の倍数+15の倍数)+30の倍数
=30/2+30/3+30/5−(30/6+30/10+30/15)+30/30
=15+10+6−(5+3+2)+1=22個
となります。答: 22個
以上