第５４問の解答

問題　［平面図形］

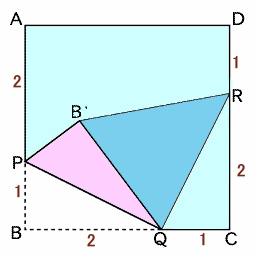問題図 左図は、正方形ＡＢＣＤを線分ＰＱで折り返したところを表しています。

また、ＡＰ：ＰＢ＝ＢＱ：ＱＣ＝ＣＲ：ＲＤ＝２：１です。

 このとき、図の△Ｂ'ＱＲの面積は正方形ＡＢＣＤの面積の何倍でしょうか。

解答例１

マサルさん

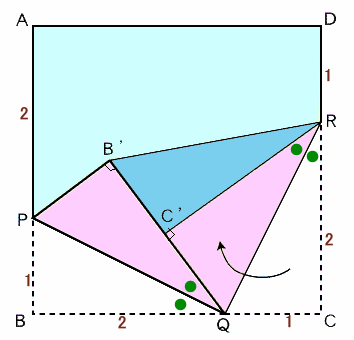
ＱＲを軸にして△ＱＲＣを折り返し、点Ｃの移動先をＣ'とします。

参考図１

△ＰＢＱと△ＱＣＲは合同より、∠ＰＱＢ＋∠ＲＱＣ＝９０゜。

よって、∠Ｂ'ＱＲ
　＝１８０゜−（∠ＰＱＢ×２＋∠ＲＱＣ）
　＝１８０°−（９０°＋∠ＰＱＢ）
　＝９０°−∠ＰＱＢ
　＝∠ＲＱＣ。

従って、Ｃ'はＢ'Ｒ上にあり、Ｃ'Ｒが△Ｂ'ＱＲの高さとなります。

よって、△ＲＣＱ
　＝１/２×Ｂ'Ｑ×Ｃ'Ｒ
　＝１/２×ＢＱ×ＣＲ
　＝１/２×（２/３×ＢＣ）×（２/３×ＣＤ）
　＝２/９×ＢＣ×ＣＤ
　＝２/９×正方形ＡＢＣＤ

答：　２/９倍

以上