第55問の解答
問題 [速さの問題]
|
|
|
|
|
|
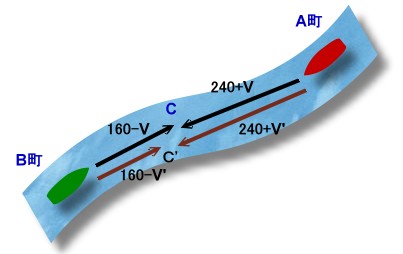
ある川の上流のA町と、そこから2km離れた下流のB町から同時に船が出発します。 A町を出発するマサル号の静水時の速さは、毎分240mで、B町を出発するハナコ号の静水時の速さは、毎分160mです。 2隻の船は途中のC橋ですれ違う予定でしたが、その日は川の流れの速さがいつもの1.5倍だったのでC橋から100m離れた地点ですれ違いました。 では、この日の川の流れの速さは毎分何mだったでしょうか。 |
|
|
|
|
|
解答例1
マサルさん
普段の川の流れをVm/分とします。
上流から下流に向かうマサル号の進む速さは、240+V。
下流から上流に向かうハナコ号の進む速さは、160−V。この両者の近づく速さ=(240+V)+(160−V)=400m/分。
従って、両者が出会うのは、2000m÷400m/分=5分後となります。さて、いつもと100m離れた地点Cで両者は出会いました。
この差は5分間でついたことになります。つまり、1分につき100m÷5分=20m/分の差がついたことになります。
これが、いつもの船の速さとの差で、川の流れの0.5倍にあたります。従って、普段の川の流れの速さは、20m/分×2=40m/分と分かります。
よって、この日の川の流れの速さ=40m/分×1.5=60m/分となります。
答: 60m/分
以上