第56問の解答
問題 [整数の性質]
|
|
|
|
|
|
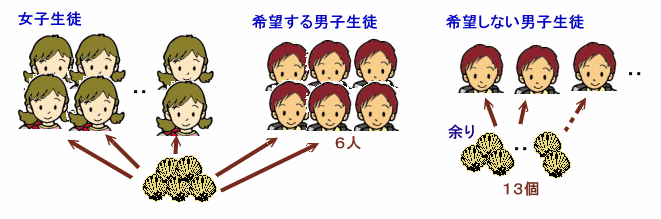
あるクラス(男女合わせて53人)のうちの女子生徒に、きれいな貝殻を同じ数ずつ配ることにしました。 はじめは女子生徒全員に同じ数ずつ余りなく配ることができたのですが、男子から「ぼくも欲しい」という意見があり、一旦全部の貝殻を回収しました。 そして、希望のあった男子6人を加えて配りなおしたところ、13個だけあまり、あと1個ずつ配ることはできませんでした。 そこで希望しなかった男子に同じ数ずつ配ることにしましたが、13個では2人分にはなっても3人分にはなりませんでした。 このクラスの女子は何人でしょうか。 |
|
|
|
|
|
解答例1
マサルさん
「そして、希望のあった男子6人を加えて配りなおしたところ、13個だけあまり、あと1個ずつ配ることはできませんでした。」から、女子生徒+6>13であることが分かります。よって、女子生徒>7です。
次に、「そこで希望しなかった男子に同じ数ずつ配ることにしましたが、13個では2人分にはなっても3人分にはなりませんでした。」ということから、配った数は一人当たり5個か6個であることが分かります。
6人の男子生徒を増やした結果、以上の現象が起こったわけです。
女子生徒の立場からすれば、男子が参加したために、自分達の一人当たりの個数を減らされたことになります。その総個数は、男子生徒に与えられた分+13個ですね。ここで、場合分けをして考えてみます。
[配った数が一人5個だった場合]
男子に配られた個数は、5個×6人=30個ですので、女子から減らされた個数は、30+13=43個。
43の約数は、1と43だけですから、女子の人数は1人と43人が考えられます。
しかし、女子生徒>7ですから、1人はダメですね。
43人の方は.....すべての条件にあてはまることになりますから、OKです。[配った数が一人6個だった場合]
男子に配られた個数は、6個×6人=36個ですので、女子から減らされた個数は、36+13=49個。
49の約数は、1と7と49ですから、女子の人数は1人と7人と49人が考えられます。
しかし、女子生徒>7ですから、1人と7人はダメですね。
49人の方は「男女合わせて53人」という条件に反します。
(男子は6人より多いので合計が53人を越してしまう.)従って、あてはまるのは43人の場合だけです。
答: 43人
以上