第57問の解答
問題 [空間図形]
|
|
|
|
|
|
|
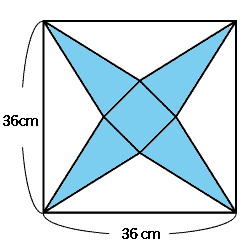 |
左図のように、一辺の長さが36cmの正方形の折り紙をもとにして、四角錐の展開図を作りました。 青い部分を切り取って組み立てると、底面が正方形で、側面がどれも二等辺三角形である正四角錐ができます。 この正四角錐の表面積が648cm2であるとき、この正四角錐の体積を求めてください。 |
|
|
|
|
|
|
解答例1
マサルさん
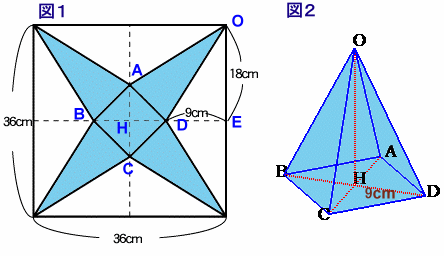
図1は問題の展開図、図2は組み立てた立体を表しています。
正四角錐の表面積が648cm2であったということは、図 1の水色の部分の面積が648cm2であったということです。
従って、白い部分の4つの三角形の面積は、
36×36−648=648cm2
であることが分かります。すると、1つの三角形は、
648÷4=162cm2
となりますね。従って、白い三角形の高さを求めることができます。
DE=162×2÷36=9cmこれで、中央の正方形ABCDの面積を求めることができます。
正方形の対角線の長さ=36−9×2=18cmですから、
面積=18×18÷2=162cm2
となります。これで、立体の底面積を求めることができました。
さて高さですが、図1の△OEDと図2の△OHDと比べてみます。
斜辺はODで共通、もう1辺はED=HD=9cmとなる直角三角形なので合同。従って、立体の高さOH=OE=18cmとなります。
よって、立体の体積=162×18÷3=972cm3となります。
答: 972cm3
以上