第59問の解答
問題 [割合]
|
|
|
|
|
|
金と銀がそれぞれ違った割合で混ぜ合わされている合金が3種類A、B、Cがあります。 はじめ、AとCを3:2の割合で混ぜて、新しい合金を作る予定でした。
しかし、間違えてCとBを3:2の割合で混ぜてしまいました。 また、AとBを3:2の割合で混ぜてみたところ、金の含有率は予定の半分であったそうです。 このとき、もとの合金A、B、Cの金の含有率の比を求めてください。 |
|
|
|
|
|
解答例1
マサルさん
天秤図で考えます。
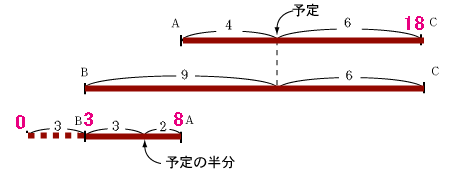
まず、1段目の線分図をご覧ください。
AとCを3:2の割合で混ぜるというのが最初の予定でした。
従って、予定の濃度はこの逆比になるので、ACを2:3=4:6に内分するところになります。次に、2段目の線分図で、「誤ってCとBを3:2の割合で混ぜてしまったところ予定の含有率になった」ところを示しています。ここ、3:2=6:9としています。予定の含有率は1段目と同じところにきますね。
3段目も同様です。今度は、AとBを3:2の割合で混ぜたところを図示しています。
1段目と2段目の線分図ではAとBの差は5と表されていますから、ちょうど分割でき、分割した部分が、予定の含有率の半分というわけです。従って、予定の含有率とその半分の差=4+2=6となります。
よって、予定の濃度=12になります。ということは、Bの左に3だけ進んだ位置に含有率0があるわけです。
すなわち、B=3と表すことができますね。
従って、A=3+5=8、C=3+5+10=18です。よって、A:B:C=8:3:18となります。
答: 8:3:18
以上