第60問の解答
問題 [推理]
|
|
|
|
|
|
あるパーティに、100組の夫婦が参加しました。 このパーティの唯一のルールは、「握手をした相手の人数を覚えておくこと。」でした。 また、夫婦同士での握手は行われないことになっています。もちろん、握手しなくてもOKです。 このパーティの参加者の一人であるマサルさんが、パーティの終了後、自分以外の199人に握手した相手の人数を聞いたところ、なんと全員の答えが異なっていたそうです。 では、マサルさんの奥さんは、何人の人と握手したと考えられるでしょうか。 |
|
|
|
|
|
解答例1
マサルさん
このパーティの参加者は全部で100×2=200人です。
「夫婦同士での握手は行わない」わけですから、握手できる最大の人数は200−2人(自分自身と自分の配偶者)=198人です。従って、可能性としては0人から198人の199通りが考えられるわけです。
マサルさんが聞いた199人は皆違った人数と握手を行ったわけですから、この199人は「誰とも握手していない人」から「198人と握手した人」までの199通り全てのパターンがちょうど当てはまることになります。
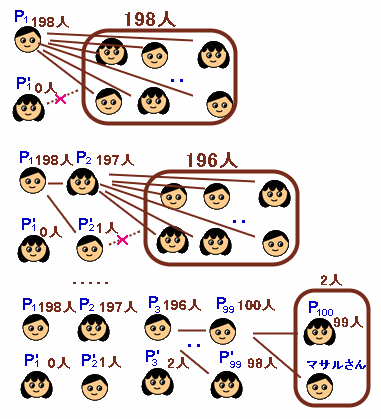
この中で、「198人と握手した人」(P1とします)を考えてみます。
P1は自分の配偶者(P'1とします)以外のすべての人と握手をしたことになります。逆に言うと、P'1以外の人は少なくとも1回は握手したことになります。
ということは、「誰とも握手しなかった人」は、P'1というになります。次に、「197人と握手した人」(P2とします)を考えます。
この人は自分の配偶者(P'2とします)とP'1の2人以外の全員と握手したことになります。こうなると、P1、P'1、P2、P'2以外の人は、最低2回(P1、P2)は握手したことになります。
ということは、「1回だけ握手した人」は、P'2ということになります。以下、同様にして、
P1・・198人と握手、 P'1・・0人と握手
P2・・197人と握手、 P'2・・1人と握手
P3・・196人と握手、 P'3・・2人と握手
・・・・
P99・・100人と握手、P'99・・98人と握手
とが、それぞれ配偶者同士の組み合わせになります。すると、マサルさん以外で残った(P100)のはマサルさんの奥さんだけです。
マサルさんの奥さん、すなわちP100は、99人と握手したことになりますが、
以上のことから、P1、P2、・・・、P99の99人と握手し、P'1、P'2、・・・P'99とは握手していませんので、
確かに99人と握手しています。答: 99人
以上