第64問の解答
問題 [平面図形]
|
|
|
|
|
|
|
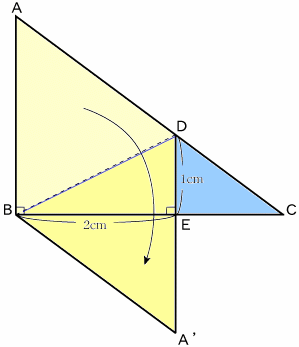 |
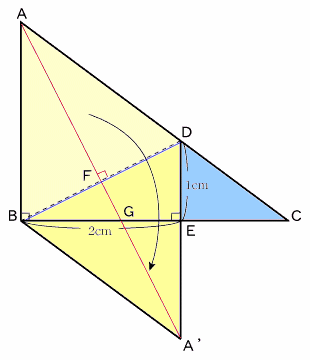
左図は、BDを軸にして直角三角形ABCを折ったところを示しています。 このとき、A'DとBCは垂直に交わっており、BE=2cm、DE=1cmとなっていました。 ここで、もとの直角三角形ABCの面積を求めてください。 |
|
|
|
|
|
|
解答例1
マサルさん
AとA'を結び、BDとの交点をF、BEとの交点をGとします。
まず、△BA'Dは、△BADを折り返したものですから、AD=A'D、AB=A'Bですね。
さらに、ともに辺BCに垂直になっているのでABとDA'は平行。また、折り返し図形の性質からAF=A'Fなので、AB=A'Dになります。
すると、四角形ABA'Dは、菱形、つまり、ADとA'Bは平行となります。
さて、△BDEと△BGFは相似な直角三角形で、直角をはさむ2辺が1:2。
従って、GF:BF=1:2。 ・・・ (1)次に、△ABFも上記の2つの三角形と相似なので、△ABFも直角をはさむ2辺が1:2。
よって、BF:FA=1:2。 ・・・ (2)従って、(1)と(2)より、GF:BF:FA=1:2:4。
また、A'F=AFより、AF:FG:GA'=4:1:3と分かります。さて、△AGCと△A'GBは相似で、AG:A'G=5:3より相似比は5:3ですね。
従って、AC:A'B=5:3。A'Bを3とすると、AC=5となります。
よって、AD=A'B=3。従って、DC=2。△DECと△A'EBの相似比は2:3より、CE:BE=2:3。
従って、CE=4/3cmと分かります。よって、BC=BE+CE=2+4/3=10/3cm。
また、AB=DE×AD/AC=5/2cm。よって、△ABC=10/3×5/2÷2=25/6cm2 となります。
答: 25/6cm2
以上