第６５問の解答

問題　［速さの問題？］

縦６０cm、横９０cm、高さ１２０cmの水槽があります。

また、この水槽には側面に一つ穴があいていて、水面が穴よりも上であればここから水が流出します。
ただし、流れ出る水量は水面の高さによらず一定であるものとします。

さて、空っぽにしたこの水槽に毎分４０リットルの割合で水を注ぎ、満水になったところで注水を止めました。
すると、穴から水が流れ出なくなるまでに、注水を止めてから２７分かかりました。
また、この作業中に流れ出た水は全部で３６０リットルでした。

では、穴は底から何cmのところにあったでしょうか。

解答例１

マサルさん

参考図１

まず、穴から水が出始めてから満水になるまでの時間を求めます。

穴から水が出始めた後に注入された水は、結局すべて流れ出てしまうことになります。
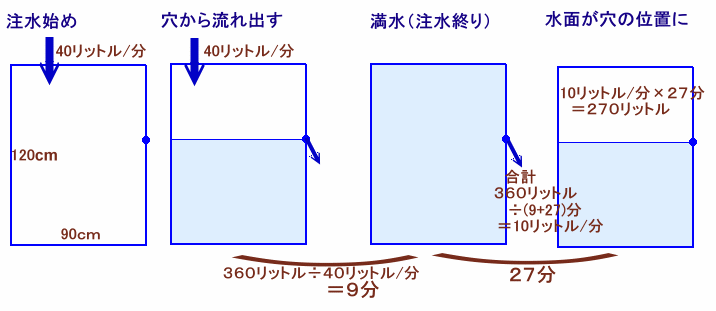
流れ出た水の量は３６０リットルで、これは毎分４０リットルの割合で注入されていますから、
　３６０リットル÷４０リットル/分＝９分
と分かります。

従って、３６０リットルの水は、９＋２７＝３６分かけて穴から流れ出たことになります。
つまり穴からは３６０リットル÷３６分＝１０リットル/分の割合で水が流れ出ていたことが分かります。

あとは穴の位置を調べることになります。

注水を止めてからの２７分間に流れ出た水の量は、
　１０リットル/分×２７分＝２７０リットル＝２７００００cm3です。

また、この水槽の底面積は６０ｃｍ×９０ｃｍ＝５４００cm2ですから、
穴の位置は、上から２７００００cm3÷５４００cm2＝５０cmと分かります。

従って、底からは、１２０−５０＝７０ｃｍとなります。

答：　７０cm

以上