第67問の解答
問題 [空間図形]
|
|
|
|
|
|
|
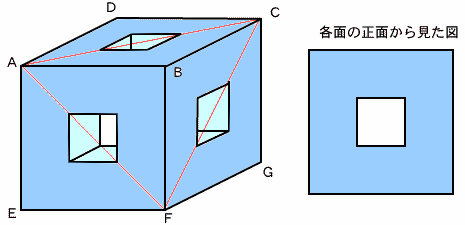 |
左図のように、立方体ABCD-EFGHの各面上に正方形の穴をあけて、向かい側の面まで突き抜けるようにします。 立方体の1辺の長さ:正方形の1辺の長さ=3:1で、正方形はそれぞれの面の中央にあけることにします。 この立体を頂点A、C、Fを通る平面で切るとき、切り口の面積は、△ACFの面積の何倍でしょうか。 |
|
|
|
|
|
|
解答例1
マサルさん
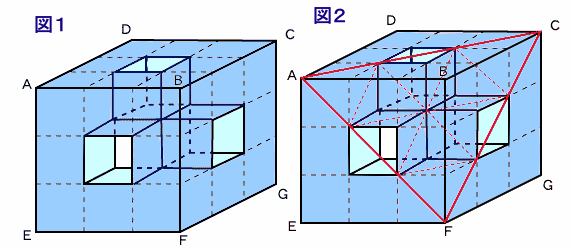
上の2つの図をご覧ください。
立方体ABCD−EFGHを3×3×3=27個の小さな立方体の集まりと考えることにします。
図1は、それを分かりやすく書いたものです。さて、立方体ABCD−EFGHの切り口は、もし空洞がなければ正三角形になります。
これは切られる小さい立方体にも言えることです。
AC、AF、CFの3辺はそれぞれ3等分されています。
なぜなら、それぞれの辺は小さい立方体の対角線3つ分だからです。そして、3等分された辺はそれぞれ、小さな正三角形の一辺となっています。
従って、切り口は図2のようになります。正三角形AFCは小さな正三角形が9個でできています。
そのうち、3個は空洞ですから、実際に切り口となっているのは6個分です。というわけで、求める面積比=6÷9=2/3となります。
答: 2/3
以上