第68問の解答
問題 [推理]
|
|
|
|
|
|
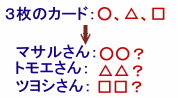
3枚のカードがあります。 それぞれのカードには1以上10以下の整数が1つ書かれています。 これを使って、以下のようなゲームを行いました。
これを数回繰り返したところ、3人の得点の合計は、 3枚のカードに書かれた数はそれぞれいくつだったでしょうか? |
|
|
|
|
|
解答例1
マサルさん
まず、ゲームの行われた回数と、3枚のカードの合計を考えます。
3人の得点の合計は、23+21+13=57点です。
カードに書かれた数は10以下より、
ゲーム回数が2以下なら、各人の得点合計は20点以下となり不適。ゲーム回数が4以上なら、57=3×19より、
ゲームの回数=19、カードの合計=3となり、カードに書かれた数は1となるので、これも不適。よって、ゲーム回数=3、カードの合計=19となります。
さて、3枚のカード合計が19であることは分かりました。
そこで、3枚のカードに書かれた数をそれぞれ、○、△、□とします。配られ方のパターンとして、○△□というのは考えられません。
なぜなら、得点が19点の人がいないからです。また、○○○とか△△△、□□□というのも考えられません。
もし考えられるとしたら3の倍数の得点(21点)をもつトモエさんだけです。さて、マサルさん、トモエさん、ツヨシくんが、それぞれ2枚(トモエさんは、2または3枚)持っているカードを、○、△、□とします。
マサルさんの3枚目は、○ではありませんので、△または□のいずれかです。
マサルさんの3枚目が△のとき
トモエさんの3枚目は○か□となりますが、○とすると、ツヨシさんの3枚目が□となり不適。
従って、次のケースのみとなります。
マサル:○○△=23 ・・・ (1)
トモエ:△△□=21 ・・・ (2)
ツヨシ:□□○=13 ・・・ (3)(1)+(2)より、
○○△△△□=44
○△□+○△△=44
○△△=44−19=25 ・・・ (4)(1)+(4)より、
○○○△△△=48
○△=48÷3=16 ・・・ (5)(1)−(5)より、○=23−16=7
よって、△=16−○=16−7=9
従って、□=21−△△=21−18=3これらは題意を満たします。
マサルさんの3枚目が□のとき
次のいずれかのケースになります。
(ケースA) (ケースB)
マサル:○○□=23 ・・・ (1) マサル:○○□=23 ・・・ (1)
トモエ:△△○=21 ・・・ (2) トモエ:△△△=21 ・・・ (2)'
ツヨシ:□□△=13 ・・・ (3) トモエ:□□○=21 ・・・ (3)'
・ケースAのとき(1)+(2)より、
○○○△△□=44
○△□+○○△=44
○○△=44−19=25 ・・・ (5)(2)+(5)より、○○○△△△=46、
よって、○△=46÷3となるが整数でないので不適。・ケースBのとき
(1)+(3)'より、
○○○□□□=44
○□=44÷3となるが整数でないので不適以上から、○=7、△=9、□=3が唯一の解となります。
答: 3、7、9
以上