第71問の解答
問題 [推理]
|
|
|
|
|
|
算チャレ共和国のわがままなマサル王子は、部下に次のような命令をしました。 「明日までに、1g〜40gまでの重さを1gおきに量ることのできる天秤をつくれ! 翌日、部下たちは命令通りの天秤を作ったそうです。 このとき、完成した天秤に用意されたおもりの重さをすべて答えてください。 |
|
|
|
|
|
解答例1
マサルさん
まず帰納的に考えてみます。
1gの重さを量れるようにするには、1gのおもりがあればOKです。
次に、2gの重さを量れるようにするわけですが、このときに考えられるのは、
A案:1gのおもりをもう一個用意する。
B案:2gのおもりを用意する。
C案:3gのおもりを用意する。
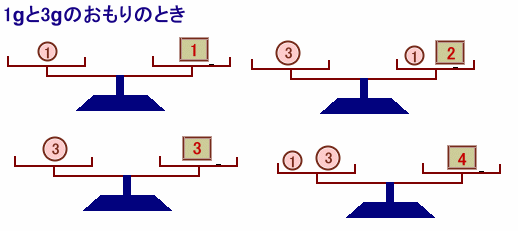
の3通りが考えられます。この中で最も効率が良いのはC案です。
なぜなら、これだと1gから4gまでの重さをすべて量ることができるようになりますから。
さて次は5gを量れるようにすればよいわけですね。
このときは、1〜9gの9通りが考えられるわけですが、もちろんここで選ぶのは9gのおもりですね。
1〜4gは既にOK。
9gと反対側に4〜1gを載せて9−4=5g〜9−1=8g、
もちろん9g自身もOK
そして、9gと同じ側に1〜4gを載せて9+1=10g〜9+4=13g以上より、1g、3g、9gの3個で1g〜13gまで量ることができます。
ここまで、3g=1g×3、9g=3g×3ですから、次は9g×3=27gのおもりと考えられます。
実際、1g、3g、9g、27gの4個で1g〜40gまで量ることができます。なぜなら、1〜13gは既にOK。
27gと反対側に13〜1gを載せて27−13=14g〜27−1=26g、
もちろん27g自身もOK
そして、27gと同じ側に1〜13gを載せて27+1=28g〜27+13=40gさて、4個が最も少ないかということについて考えてみましょう。
そこで、n個のおもりがあるときに、最大何通りの重さを量ることができるのかを考えてみます。n個のおもりがあるとき、このおもりの使い方は、左の皿に載せる、右の皿に載せる、載せないの3通りがあります。従って、合計3n通りの使い方が考えられることになります。
しかし、これだとおもりを全く載せない場合が含まれているので、これを除く3n-1通りとします。
さらに、これらには、左右ちょうど反対となる組み合わせがダブって数えています。
例えば右に1g、左に3gの場合と右に3g、左に1gの場合は、どちらも2gを量ることになります。従って、重複を除くと、n個のおもりで量ることのできる重さは最大で(3n-1)/2通りであることが分か
ります。n=3のときは、(33-1)/2=13通り、n=4のときは、(34-1)/2=40通りと分かりますから、
40通りを量るには少なくとも4個のおもりが必要となります。
答: 1g、3g、9g、27g
以上