第72問の解答
問題 [速さの問題]
|
|
|
|
|
|
ボートに乗ったマサルさんとツヨシ君がある川のP地点にいます。
はじめ、2人はP地点から上流にむかって同時に出発しました。 次に、2人はQ地点から下流にむかって同時に出発しました。 流れのない水上でのボートの速さは、マサル君は毎分90m、ツヨシ君は毎分70mです。 |
|
|
|
|
|
解答例1
マサルさん
まず、行きについて考えてみましょう。
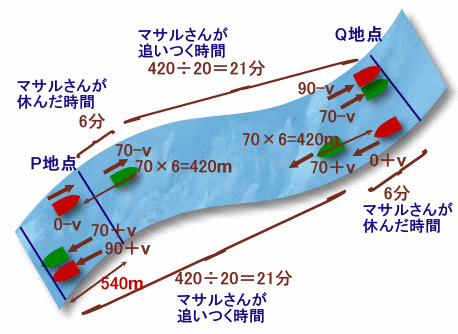
マサルさんは途中で6分間休みました。
(こういうときは、初めに6分間休んじゃったと考えるとイメージがわきやすいですね。)
この間にどの程度の差がついてしまったのかを考えます。川の流れの速さVで押し戻されているというのは2人とも同じ条件ですね。
すると、マサルさんがこぐのを休んでいる間の2人の速さは、
マサルさん ・・・・ 0m/分−川の流れの速さ
ツヨシ君 ・・・・ 70m/分−川の流れの速さ
ということになります。ということは、2人の速さの差は70m/分ですね。
ということは、マサルさんが休んでいる間に、ツヨシ君は70m/分×6分=420mほどマサルさんに差をつけたことになります。
その後、Q地点でマサルさんはツヨシ君に追いついたわけです。
2人ともボートをこいでいるとき、速さの差は90−70=20m/分です。
となると、マサルさんがツヨシ君に追いつくには、420÷20=21分かかることになります。つまり、2人がQ地点に到着したのは、P地点を出発後21+6=27分であることが分かりま
す。帰りの場合も全く同じですね。
マサルさんが休んでいる間についた差は420m。そして追いつくのにかかる時間が21分。
で、2人は出発後21+6=27分でP地点の下流540mの地点に到着したことになります。さて、上流に向かう場合も下流に向かう場合も27分かかっていることが分かりました。
しかし、その間に進んだ距離は540mの差があります。
この理由はもちろん、川の流れの速さVにあります。つまり、上流に向かう際には、押し戻されるために速度は遅くなり、下流に向かう際には後押しされるために速度は速くなります。
それぞれ27分進んだ結果、着いた差が540mですから、1分あたりの差は20mです。
これは川の流れの速さVの2倍にあたりますね。
つまり、川の流れの速さV=10m/分ということが分かります。従って、ツヨシ君が上流に向かうときの速さは70−10=60m/分ですね。
で、ツヨシ君は27分でQ地点に到着したわけですから、
PQ間の距離は、 60m/分×27分=1620mとなります。答: 1620m
以上